lim-x-0-sinx-tanx-

Question Number 28088 by tawa tawa last updated on 20/Jan/18

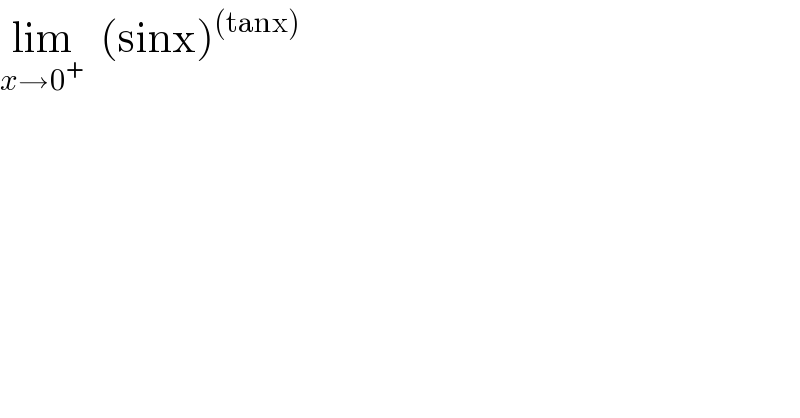
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\:\left(\mathrm{sinx}\right)^{\left(\mathrm{tanx}\right)} \\ $$

Commented by çhëý böý last updated on 20/Jan/18

lim_(x→0^+ ) e^(ln sinx^(tanx) ) e^(lim_(x→0^+ ) tan xln x) l′hopital e^(lim_(x→0+) − (((cosx)/(sinx))/((sec^2 x)/(tan^2 x)))) simplify e^(lim_(x→0^(+ ) ) −((sinx)/(cos^3 x))) e^(lim_(x→0^+ ) − ((sin(0))/(cos(0)^3 )) = ((−0)/1) =0) e^(0 ) =1

$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\:\:{e}^{\mathrm{ln}\:\mathrm{sin}{x}^{{tanx}} } \:\:\: \\ $$$$\boldsymbol{{e}}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\mathrm{tan}\:\boldsymbol{{x}}\mathrm{ln}\:\boldsymbol{{x}}} \\ $$$$\:\:\:\: \\ $$$$\boldsymbol{{l}}'{hopital} \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\:\:−\:\frac{\frac{{cosx}}{{sinx}}}{\frac{{sec}^{\mathrm{2}} {x}}{{tan}^{\mathrm{2}} {x}}}} \\ $$$$ \\ $$$${simplify} \\ $$$$ \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}^{+\:} \:\:} {\mathrm{lim}}\:−\frac{{sinx}}{{cos}^{\mathrm{3}} {x}}} \: \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:−\:\frac{{sin}\left(\mathrm{0}\right)}{{cos}\left(\mathrm{0}\right)^{\mathrm{3}} }\:=\:\:\frac{−\mathrm{0}}{\mathrm{1}}\:=\mathrm{0}} \:\: \\ $$$${e}^{\mathrm{0}\:} =\mathrm{1} \\ $$$$ \\ $$

Commented by abdo imad last updated on 20/Jan/18

x→0^+ mean x is most near from 0 and x>0 x→0− mean that x is most near from 0 and x<0 .

$${x}\rightarrow\mathrm{0}^{+} \:\:{mean}\:\:{x}\:{is}\:{most}\:{near}\:{from}\:\mathrm{0}\:{and}\:{x}>\mathrm{0} \\ $$$${x}\rightarrow\mathrm{0}−\:{mean}\:{that}\:{x}\:{is}\:{most}\:{near}\:{from}\:\mathrm{0}\:{and}\:{x}<\mathrm{0}\:. \\ $$

Commented by tawa tawa last updated on 20/Jan/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by tawa tawa last updated on 20/Jan/18

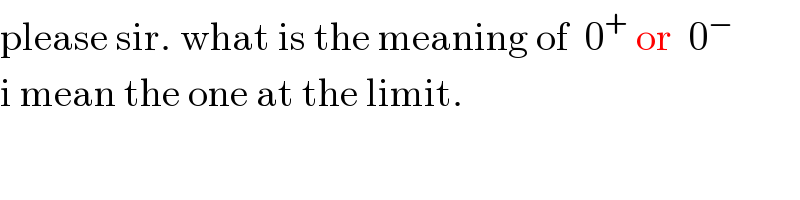
please sir. what is the meaning of 0^+ or 0^− i mean the one at the limit.

$$\mathrm{please}\:\mathrm{sir}.\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{meaning}\:\mathrm{of}\:\:\mathrm{0}^{+} \:\mathrm{or}\:\:\mathrm{0}^{−} \\ $$$$\mathrm{i}\:\mathrm{mean}\:\mathrm{the}\:\mathrm{one}\:\mathrm{at}\:\mathrm{the}\:\mathrm{limit}. \\ $$

Commented by çhëý böý last updated on 20/Jan/18

it mean the limit can^′ t at 0 so 0^(+ ) mean u ar approching from right[positive] side

$${it}\:{mean}\:{the}\:{limit}\:{can}^{'} {t}\:{at}\:\mathrm{0}\:{so}\:\mathrm{0}^{+\:} {mean} \\ $$$${u}\:{ar}\:{approching}\:{from}\:{right}\left[{positive}\right]\:{side} \\ $$

Commented by abdo imad last updated on 20/Jan/18

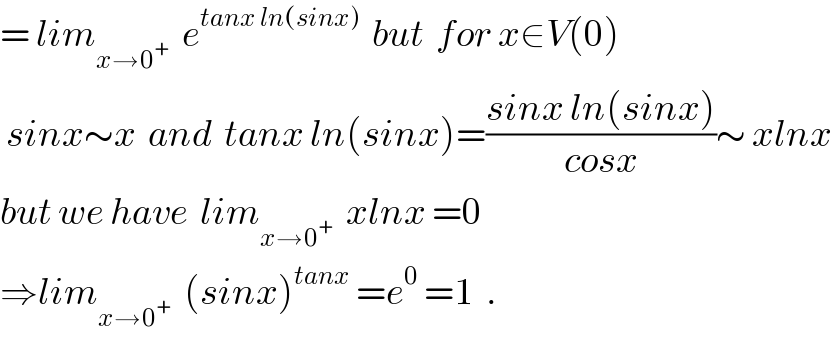
= lim_(x→0^+ ) e^(tanx ln(sinx)) but for x∈V(0) sinx∼x and tanx ln(sinx)=((sinx ln(sinx))/(cosx))∼ xlnx but we have lim_(x→0^+ ) xlnx =0 ⇒lim_(x→0^+ ) (sinx)^(tanx) =e^0 =1 .

$$=\:{lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:{e}^{{tanx}\:{ln}\left({sinx}\right)} \:\:{but}\:\:{for}\:{x}\in{V}\left(\mathrm{0}\right) \\ $$$$\:{sinx}\sim{x}\:\:{and}\:\:{tanx}\:{ln}\left({sinx}\right)=\frac{{sinx}\:{ln}\left({sinx}\right)}{{cosx}}\sim\:{xlnx} \\ $$$${but}\:{we}\:{have}\:\:{lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:{xlnx}\:=\mathrm{0} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\left({sinx}\right)^{{tanx}} \:={e}^{\mathrm{0}} \:=\mathrm{1}\:\:. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply