Question Number 163825 by cortano1 last updated on 11/Jan/22
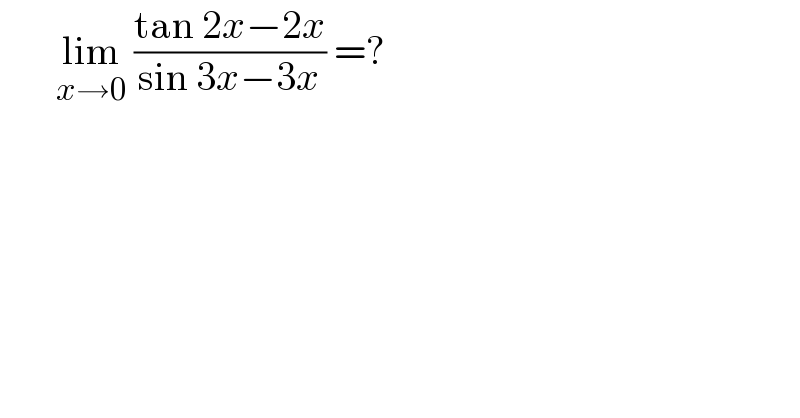
$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\mathrm{2}{x}−\mathrm{2}{x}}{\mathrm{sin}\:\mathrm{3}{x}−\mathrm{3}{x}}\:=?\: \\ $$
Answered by Ar Brandon last updated on 11/Jan/22
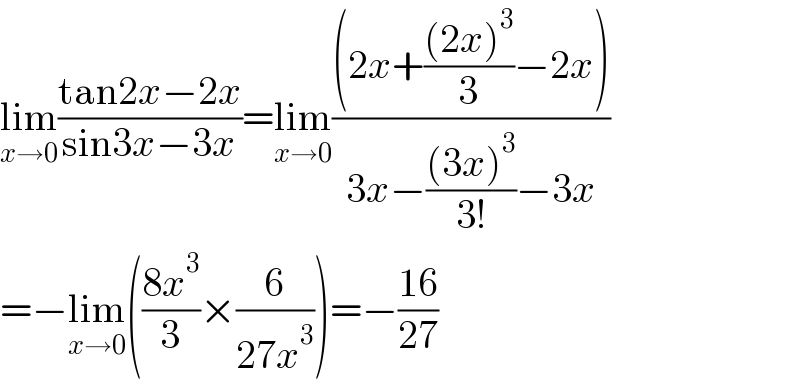
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan2}{x}−\mathrm{2}{x}}{\mathrm{sin3}{x}−\mathrm{3}{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{2}{x}+\frac{\left(\mathrm{2}{x}\right)^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}{x}\right)}{\mathrm{3}{x}−\frac{\left(\mathrm{3}{x}\right)^{\mathrm{3}} }{\mathrm{3}!}−\mathrm{3}{x}} \\ $$$$=−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{8}{x}^{\mathrm{3}} }{\mathrm{3}}×\frac{\mathrm{6}}{\mathrm{27}{x}^{\mathrm{3}} }\right)=−\frac{\mathrm{16}}{\mathrm{27}} \\ $$
Answered by bobhans last updated on 11/Jan/22
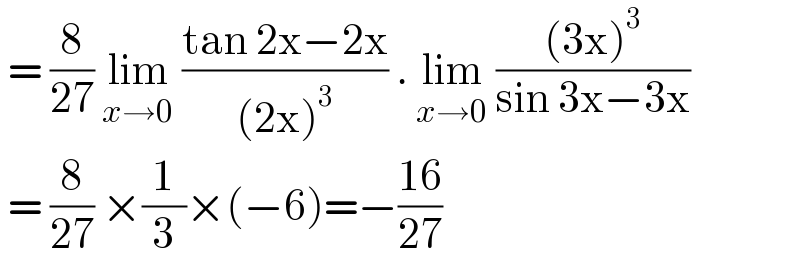
$$\:=\:\frac{\mathrm{8}}{\mathrm{27}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\mathrm{2x}−\mathrm{2x}}{\left(\mathrm{2x}\right)^{\mathrm{3}} }\:.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{3x}\right)^{\mathrm{3}} }{\mathrm{sin}\:\mathrm{3x}−\mathrm{3x}}\: \\ $$$$\:=\:\frac{\mathrm{8}}{\mathrm{27}}\:×\frac{\mathrm{1}}{\mathrm{3}}×\left(−\mathrm{6}\right)=−\frac{\mathrm{16}}{\mathrm{27}} \\ $$
