Question Number 87378 by jagoll last updated on 04/Apr/20
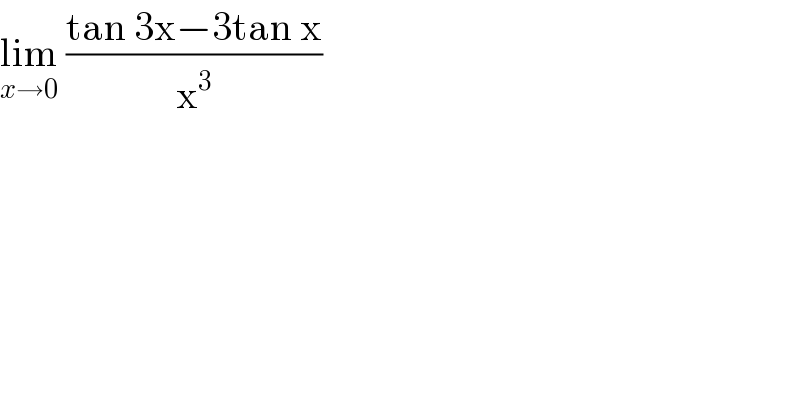
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\mathrm{3x}−\mathrm{3tan}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} } \\ $$
Commented by john santu last updated on 04/Apr/20
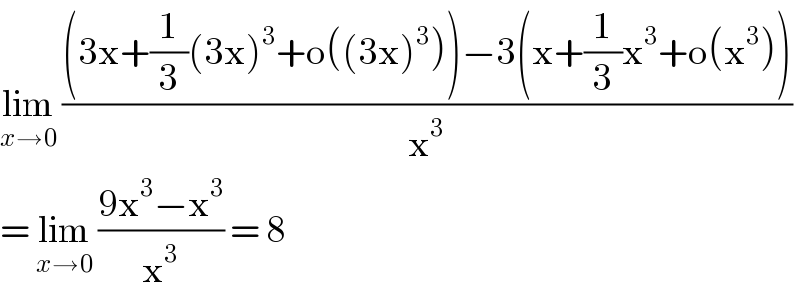
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{3x}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{3x}\right)^{\mathrm{3}} +\mathrm{o}\left(\left(\mathrm{3x}\right)^{\mathrm{3}} \right)\right)−\mathrm{3}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{3}} \right)\right)}{\mathrm{x}^{\mathrm{3}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{9x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{8} \\ $$
Answered by ajfour last updated on 04/Apr/20
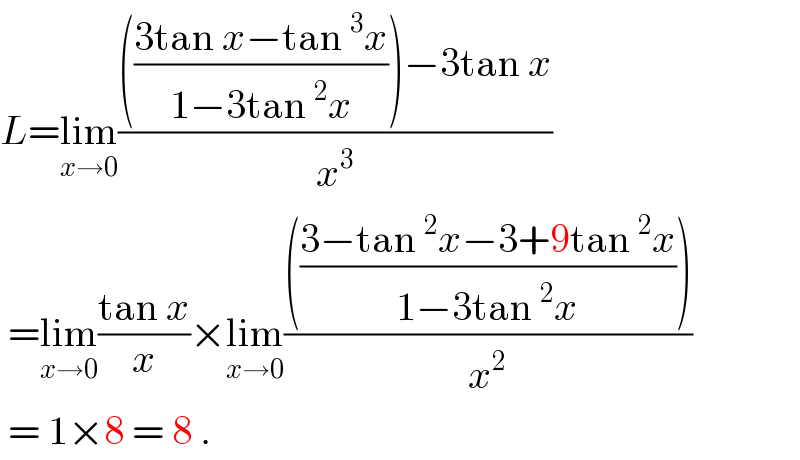
$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{3tan}\:{x}−\mathrm{tan}\:^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{3tan}\:^{\mathrm{2}} {x}}\right)−\mathrm{3tan}\:{x}}{{x}^{\mathrm{3}} } \\ $$$$\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:{x}}{{x}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{3}−\mathrm{tan}\:^{\mathrm{2}} {x}−\mathrm{3}+\mathrm{9tan}\:^{\mathrm{2}} {x}}{\mathrm{1}−\mathrm{3tan}\:^{\mathrm{2}} {x}}\right)}{{x}^{\mathrm{2}} } \\ $$$$\:=\:\mathrm{1}×\mathrm{8}\:=\:\mathrm{8}\:. \\ $$
Commented by peter frank last updated on 04/Apr/20

$${thank}\:{you} \\ $$
Commented by jagoll last updated on 04/Apr/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3tan}\:\mathrm{x}−\mathrm{tan}\:^{\mathrm{3}} \mathrm{x}\:−\mathrm{3tan}\:\mathrm{x}+\mathrm{9tan}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{8tan}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{8}\:\leftarrow\:\mathrm{the}\:\mathrm{ans} \\ $$
Commented by jagoll last updated on 04/Apr/20
$$\mathrm{haha}..\mathrm{same}\:\mathrm{sir}.\:\mathrm{typo} \\ $$
Commented by ajfour last updated on 04/Apr/20
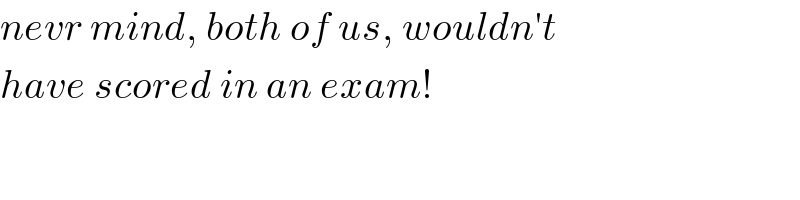
$${nevr}\:{mind},\:{both}\:{of}\:{us},\:{wouldn}'{t} \\ $$$${have}\:{scored}\:{in}\:{an}\:{exam}! \\ $$
