Question Number 105614 by bemath last updated on 30/Jul/20
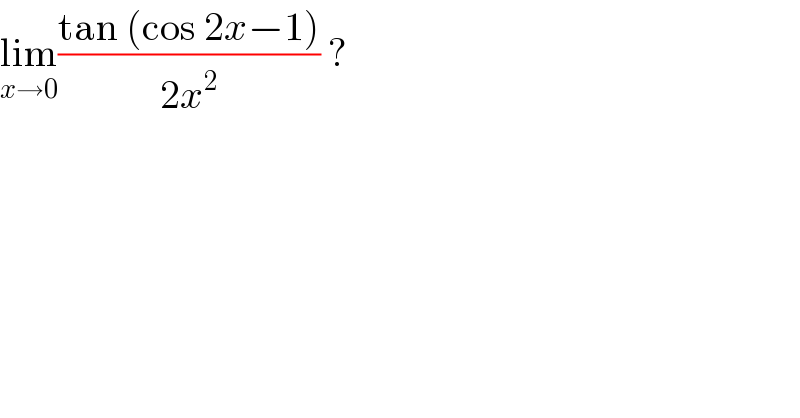
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:\left(\mathrm{cos}\:\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{2}} }\:? \\ $$
Commented by PRITHWISH SEN 2 last updated on 30/Jul/20
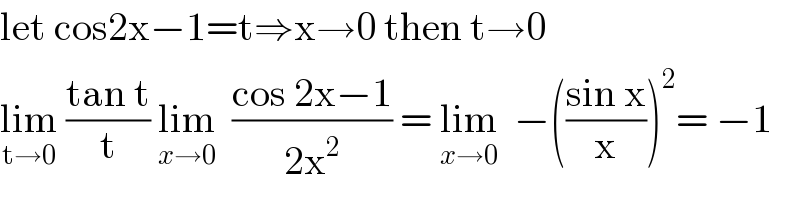
$$\mathrm{let}\:\mathrm{cos2x}−\mathrm{1}=\mathrm{t}\Rightarrow\mathrm{x}\rightarrow\mathrm{0}\:\mathrm{then}\:\mathrm{t}\rightarrow\mathrm{0} \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\mathrm{t}}{\mathrm{t}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{cos}\:\mathrm{2x}−\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:−\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)^{\mathrm{2}} =\:−\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 30/Jul/20
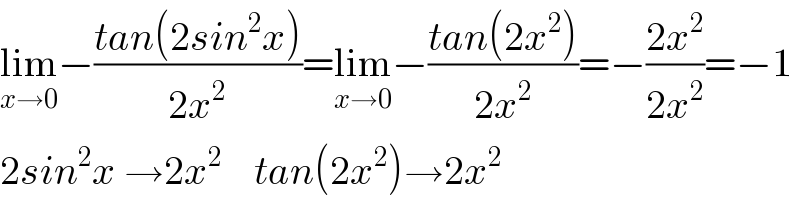
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{{tan}\left(\mathrm{2}{sin}^{\mathrm{2}} {x}\right)}{\mathrm{2}{x}^{\mathrm{2}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{{tan}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{\mathrm{2}{x}^{\mathrm{2}} }=−\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }=−\mathrm{1} \\ $$$$\mathrm{2}{sin}^{\mathrm{2}} {x}\:\rightarrow\mathrm{2}{x}^{\mathrm{2}} \:\:\:\:{tan}\left(\mathrm{2}{x}^{\mathrm{2}} \right)\rightarrow\mathrm{2}{x}^{\mathrm{2}} \\ $$
Answered by bobhans last updated on 30/Jul/20
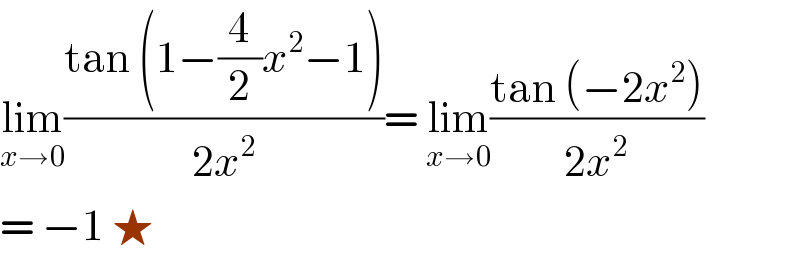
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:\left(\mathrm{1}−\frac{\mathrm{4}}{\mathrm{2}}{x}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{2}} }=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:\left(−\mathrm{2}{x}^{\mathrm{2}} \right)}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$=\:−\mathrm{1}\:\bigstar \\ $$
