Question Number 161760 by cortano last updated on 22/Dec/21
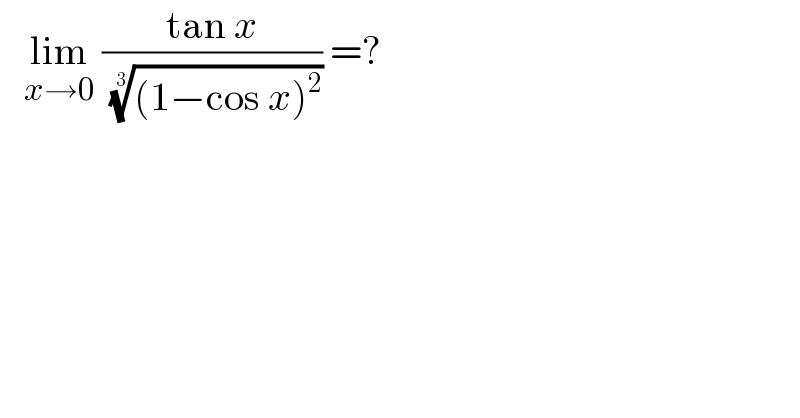
$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:{x}}{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{1}−\mathrm{cos}\:{x}\right)^{\mathrm{2}} }}\:=? \\ $$
Answered by Ar Brandon last updated on 22/Dec/21
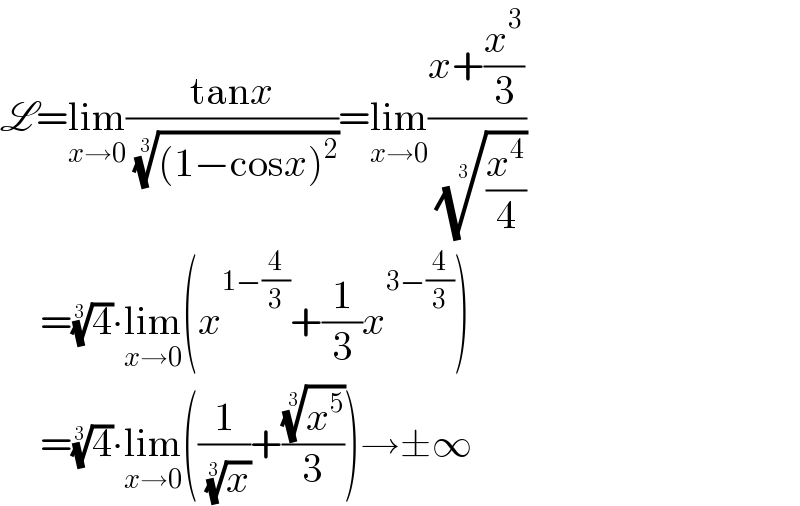
$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}{x}}{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{1}−\mathrm{cos}{x}\right)^{\mathrm{2}} }}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}{\:\sqrt[{\mathrm{3}}]{\frac{{x}^{\mathrm{4}} }{\mathrm{4}}}} \\ $$$$\:\:\:\:\:=\sqrt[{\mathrm{3}}]{\mathrm{4}}\centerdot\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({x}^{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}} +\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}−\frac{\mathrm{4}}{\mathrm{3}}} \right) \\ $$$$\:\:\:\:\:=\sqrt[{\mathrm{3}}]{\mathrm{4}}\centerdot\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{x}}}+\frac{\sqrt[{\mathrm{3}}]{{x}^{\mathrm{5}} }}{\mathrm{3}}\right)\rightarrow\pm\infty \\ $$
