Question Number 160912 by cortano last updated on 09/Dec/21
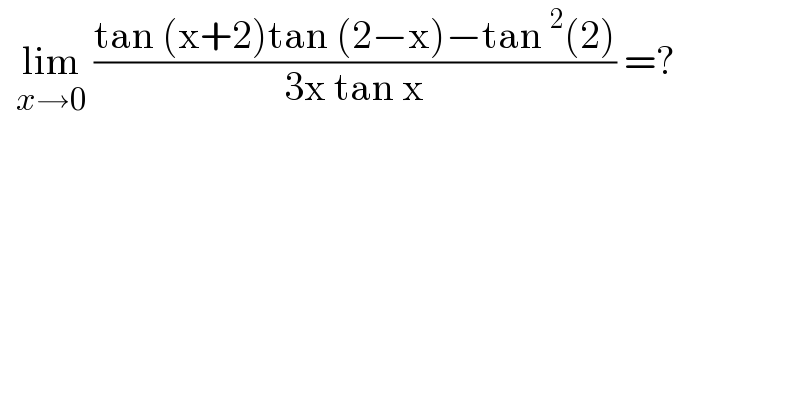
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\mathrm{x}+\mathrm{2}\right)\mathrm{tan}\:\left(\mathrm{2}−\mathrm{x}\right)−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{3x}\:\mathrm{tan}\:\mathrm{x}}\:=? \\ $$
Answered by blackmamba last updated on 09/Dec/21

$$\:\begin{cases}{\mathrm{tan}\:\left({x}+\mathrm{2}\right)=\frac{\mathrm{tan}\:\mathrm{2}+\mathrm{tan}\:{x}}{\mathrm{1}−\mathrm{tan}\:\mathrm{2}\:\mathrm{tan}\:{x}}}\\{\mathrm{tan}\:\left(\mathrm{2}−{x}\right)=\frac{\mathrm{tan}\:\mathrm{2}−\mathrm{tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:\mathrm{2}\:\mathrm{tan}\:{x}}}\\{\mathrm{tan}\:\left({x}+\mathrm{2}\right)\mathrm{tan}\:\left(\mathrm{2}−{x}\right)=\frac{\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{tan}\:^{\mathrm{2}} \left({x}\right)}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)\mathrm{tan}\:^{\mathrm{2}} \left({x}\right)}}\end{cases} \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{tan}\:^{\mathrm{2}} \left({x}\right)}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)\:\mathrm{tan}\:^{\mathrm{2}} \left({x}\right)}\:−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{3}{x}\:\mathrm{tan}\:{x}}\: \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{tan}\:^{\mathrm{2}} \left({x}\right)+\mathrm{tan}\:^{\mathrm{2}} \left({x}\right)\mathrm{tan}\:^{\mathrm{4}} \left(\mathrm{2}\right)}{\mathrm{3}{x}\:\mathrm{tan}\:{x}\:\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)\mathrm{tan}\:^{\mathrm{2}} \left({x}\right)\right)} \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:^{\mathrm{2}} \left({x}\right)}{\mathrm{3}{x}\:\mathrm{tan}\:{x}}\:.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{tan}\:^{\mathrm{4}} \left(\mathrm{2}\right)−\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)\:\mathrm{tan}\:^{\mathrm{2}} \left({x}\right)}\right) \\ $$$$\:=\:\frac{\mathrm{tan}\:^{\mathrm{4}} \left(\mathrm{2}\right)−\mathrm{1}}{\mathrm{3}} \\ $$
