Question Number 104217 by bemath last updated on 20/Jul/20
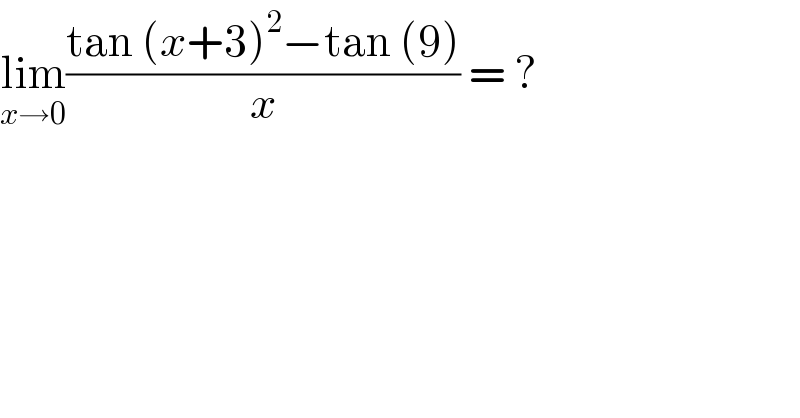
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:\left({x}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{tan}\:\left(\mathrm{9}\right)}{{x}}\:=\:? \\ $$
Answered by bemath last updated on 20/Jul/20
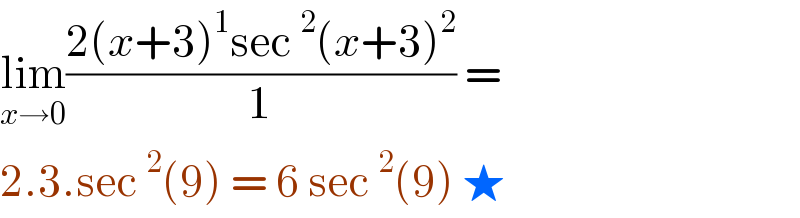
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left({x}+\mathrm{3}\right)^{\mathrm{1}} \mathrm{sec}\:^{\mathrm{2}} \left({x}+\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{1}}\:= \\ $$$$\mathrm{2}.\mathrm{3}.\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{9}\right)\:=\:\mathrm{6}\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{9}\right)\:\bigstar\: \\ $$
Answered by Dwaipayan Shikari last updated on 20/Jul/20
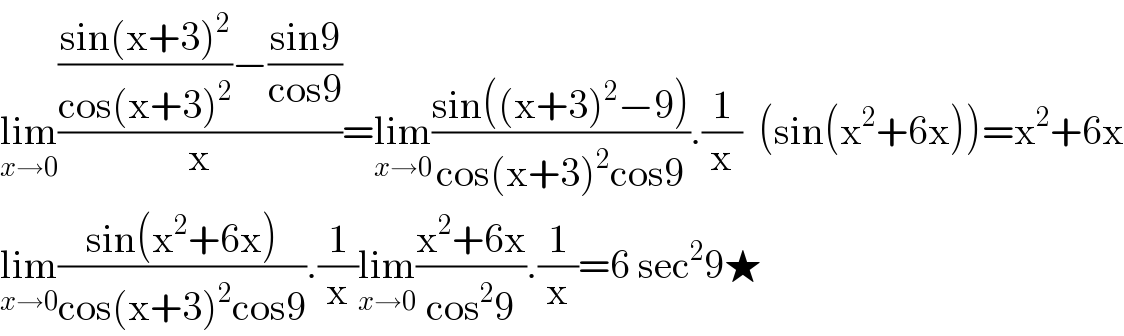
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{sin}\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{cos}\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} }−\frac{\mathrm{sin9}}{\mathrm{cos9}}}{\mathrm{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{9}\right)}{\mathrm{cos}\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} \mathrm{cos9}}.\frac{\mathrm{1}}{\mathrm{x}}\:\:\left(\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{6x}\right)\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{6x} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{6x}\right)}{\mathrm{cos}\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} \mathrm{cos9}}.\frac{\mathrm{1}}{\mathrm{x}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{6x}}{\mathrm{cos}^{\mathrm{2}} \mathrm{9}}.\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{6}\:\mathrm{sec}^{\mathrm{2}} \mathrm{9}\bigstar \\ $$
