Menu Close

lim-x-0-tan-x-4tan-2x-3tan-3x-x-2-tan-x-

Tinku Tara 0 Comments
Pin




Question Number 173225 by cortano1 last updated on 08/Jul/22
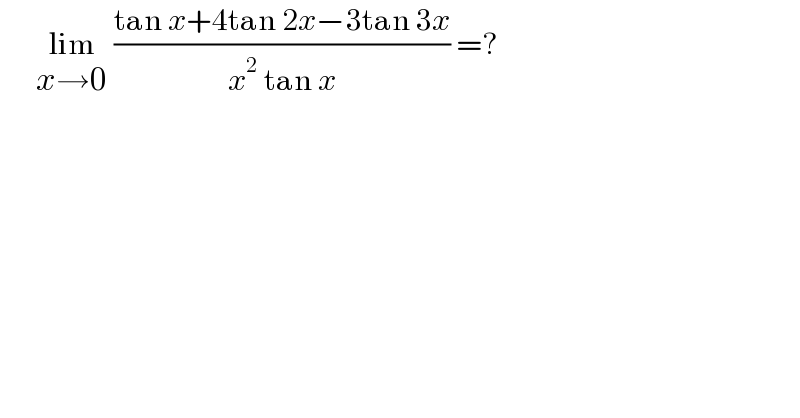
lim_(x→0) ((tan x+4tan 2x−3tan 3x)/(x^2 tan x)) =?
$$\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:{x}+\mathrm{4tan}\:\mathrm{2}{x}−\mathrm{3tan}\:\mathrm{3}{x}}{{x}^{\mathrm{2}} \:\mathrm{tan}\:{x}}\:=?\: \\ $$
Answered by floor(10²Eta[1]) last updated on 08/Jul/22
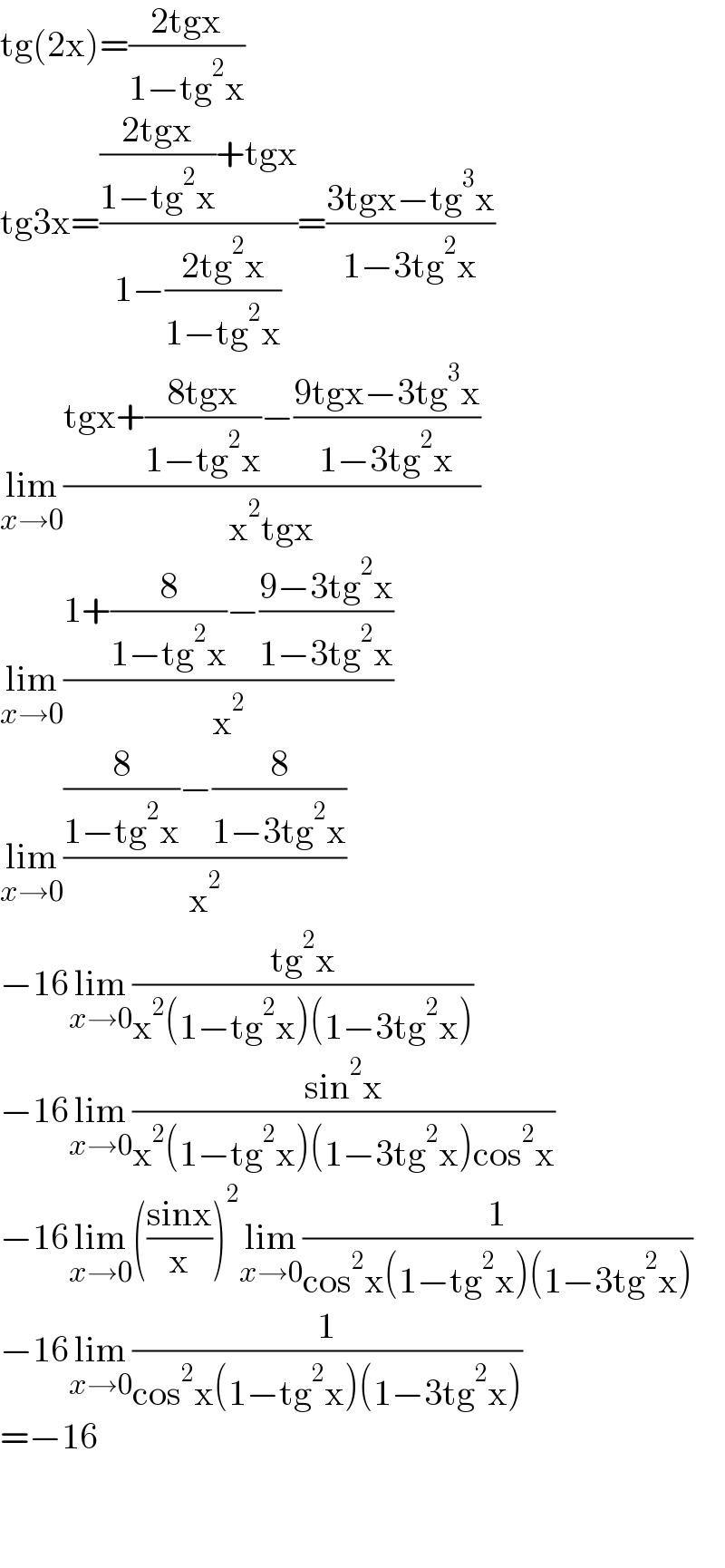
tg(2x)=((2tgx)/(1−tg^2 x)) tg3x=((((2tgx)/(1−tg^2 x))+tgx)/(1−((2tg^2 x)/(1−tg^2 x))))=((3tgx−tg^3 x)/(1−3tg^2 x)) lim_(x→0) ((tgx+((8tgx)/(1−tg^2 x))−((9tgx−3tg^3 x)/(1−3tg^2 x)))/(x^2 tgx)) lim_(x→0) ((1+(8/(1−tg^2 x))−((9−3tg^2 x)/(1−3tg^2 x)))/x^2 ) lim_(x→0) (((8/(1−tg^2 x))−(8/(1−3tg^2 x)))/x^2 ) −16lim_(x→0) ((tg^2 x)/(x^2 (1−tg^2 x)(1−3tg^2 x))) −16lim_(x→0) ((sin^2 x)/(x^2 (1−tg^2 x)(1−3tg^2 x)cos^2 x)) −16lim_(x→0) (((sinx)/x))^2 lim_(x→0) (1/(cos^2 x(1−tg^2 x)(1−3tg^2 x))) −16lim_(x→0) (1/(cos^2 x(1−tg^2 x)(1−3tg^2 x))) =−16
$$\mathrm{tg}\left(\mathrm{2x}\right)=\frac{\mathrm{2tgx}}{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}} \\ $$$$\mathrm{tg3x}=\frac{\frac{\mathrm{2tgx}}{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}}+\mathrm{tgx}}{\mathrm{1}−\frac{\mathrm{2tg}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}}}=\frac{\mathrm{3tgx}−\mathrm{tg}^{\mathrm{3}} \mathrm{x}}{\mathrm{1}−\mathrm{3tg}^{\mathrm{2}} \mathrm{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tgx}+\frac{\mathrm{8tgx}}{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}}−\frac{\mathrm{9tgx}−\mathrm{3tg}^{\mathrm{3}} \mathrm{x}}{\mathrm{1}−\mathrm{3tg}^{\mathrm{2}} \mathrm{x}}}{\mathrm{x}^{\mathrm{2}} \mathrm{tgx}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\frac{\mathrm{8}}{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}}−\frac{\mathrm{9}−\mathrm{3tg}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{3tg}^{\mathrm{2}} \mathrm{x}}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{8}}{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}}−\frac{\mathrm{8}}{\mathrm{1}−\mathrm{3tg}^{\mathrm{2}} \mathrm{x}}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$−\mathrm{16}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tg}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}−\mathrm{3tg}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$−\mathrm{16}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}−\mathrm{3tg}^{\mathrm{2}} \mathrm{x}\right)\mathrm{cos}^{\mathrm{2}} \mathrm{x}} \\ $$$$−\mathrm{16}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)^{\mathrm{2}} \underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}−\mathrm{3tg}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$−\mathrm{16}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}−\mathrm{3tg}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$=−\mathrm{16} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *