Question Number 130869 by EDWIN88 last updated on 30/Jan/21
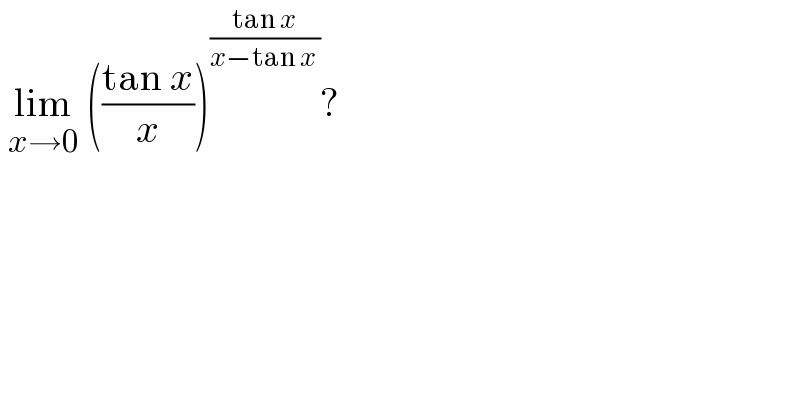
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{tan}\:{x}}{{x}}\right)^{\frac{\mathrm{tan}\:{x}}{{x}−\mathrm{tan}\:{x}\:}} ? \\ $$
Answered by benjo_mathlover last updated on 30/Jan/21
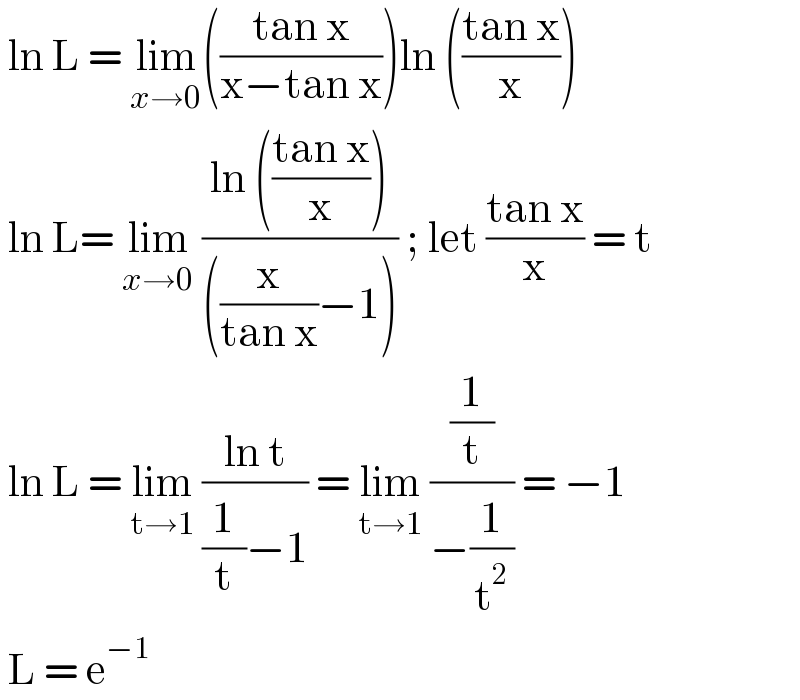
$$\:\mathrm{ln}\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{x}−\mathrm{tan}\:\mathrm{x}}\right)\mathrm{ln}\:\left(\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{x}}\right) \\ $$$$\:\mathrm{ln}\:\mathrm{L}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{x}}\right)}{\left(\frac{\mathrm{x}}{\mathrm{tan}\:\mathrm{x}}−\mathrm{1}\right)}\:;\:\mathrm{let}\:\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{x}}\:=\:\mathrm{t} \\ $$$$\:\mathrm{ln}\:\mathrm{L}\:=\:\underset{\mathrm{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\mathrm{t}}{\frac{\mathrm{1}}{\mathrm{t}}−\mathrm{1}}\:=\:\underset{\mathrm{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{t}}}{−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\:=\:−\mathrm{1} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}^{−\mathrm{1}} \: \\ $$
