Question Number 148986 by mathdanisur last updated on 02/Aug/21
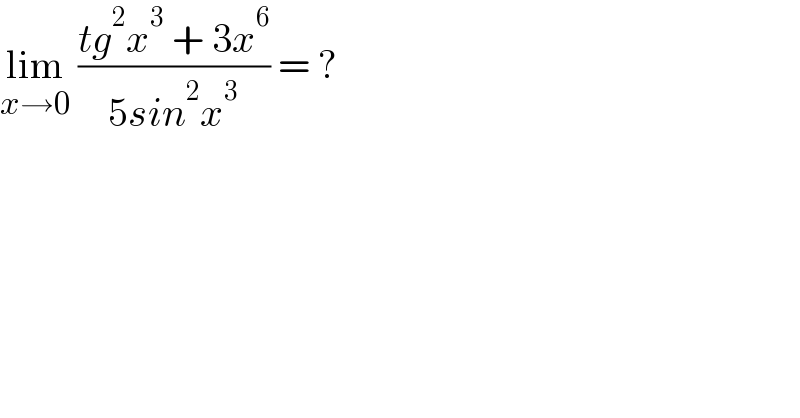
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{tg}^{\mathrm{2}} {x}^{\mathrm{3}} \:+\:\mathrm{3}{x}^{\mathrm{6}} }{\mathrm{5}{sin}^{\mathrm{2}} {x}^{\mathrm{3}} }\:=\:? \\ $$
Answered by EDWIN88 last updated on 02/Aug/21

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{tan}\:{x}^{\mathrm{3}} \right)^{\mathrm{2}} −\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{6}} }{\mathrm{5}\left(\mathrm{sin}\:{x}^{\mathrm{3}} \right)^{\mathrm{2}} \:} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{tan}\:{x}^{\mathrm{3}} −{x}^{\mathrm{3}} \right)\left(\mathrm{tan}\:{x}^{\mathrm{3}} +{x}^{\mathrm{3}} \right)+\mathrm{4}{x}^{\mathrm{6}} }{\mathrm{5}\left(\mathrm{sin}\:{x}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{tan}\:{x}^{\mathrm{3}} −{x}^{\mathrm{3}} \right)}{\mathrm{5sin}\:{x}^{\mathrm{3}} }\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:{x}^{\mathrm{3}} +{x}^{\mathrm{3}} }{\mathrm{sin}\:{x}^{\mathrm{3}} }+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{4}{x}^{\mathrm{6}} }{\mathrm{5sin}\:^{\mathrm{2}} {x}^{\mathrm{3}} } \\ $$$$=\:\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:{u}−{u}}{\mathrm{5sin}\:{u}}×\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:{u}+{u}}{\mathrm{sin}\:{u}}\:+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{4}}{\mathrm{5}\left(\frac{\mathrm{sin}\:{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} }\right)^{\mathrm{2}} } \\ $$$$=\:\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{u}−{u}\mathrm{cos}\:{u}}{\mathrm{5sin}\:{u}}×\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{u}+{u}\mathrm{cos}\:{u}}{\mathrm{sin}\:{u}}\:+\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}+\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{u}−{u}+{u}−{u}\mathrm{cos}\:{u}}{\mathrm{5sin}\:{u}}×\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{u}−{u}+{u}+{u}\mathrm{cos}\:{u}}{\mathrm{sin}\:{u}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{sin}\:{u}−{u}}{{u}^{\mathrm{3}} }\right){u}^{\mathrm{3}} +{u}\left(\mathrm{1}−\mathrm{cos}\:{u}\right)}{\mathrm{sin}\:{u}}×\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{sin}\:{u}−{u}}{{u}^{\mathrm{3}} }\right){u}^{\mathrm{3}} +{u}\left(\mathrm{1}+\mathrm{cos}\:{u}\right)}{\mathrm{sin}\:{u}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{u}^{\mathrm{3}} +{u}\left(\mathrm{2sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}{u}\right)}{\mathrm{sin}\:{u}}×\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{u}^{\mathrm{3}} +{u}\left(−\mathrm{2sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}{u}\right)}{\mathrm{sin}\:{u}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}×\mathrm{0}×\mathrm{0}\:=\:\frac{\mathrm{4}}{\mathrm{5}} \\ $$
Commented by mathdanisur last updated on 02/Aug/21

$${Thank}\:{You}\:{Ser} \\ $$
