Question Number 161361 by cortano last updated on 17/Dec/21
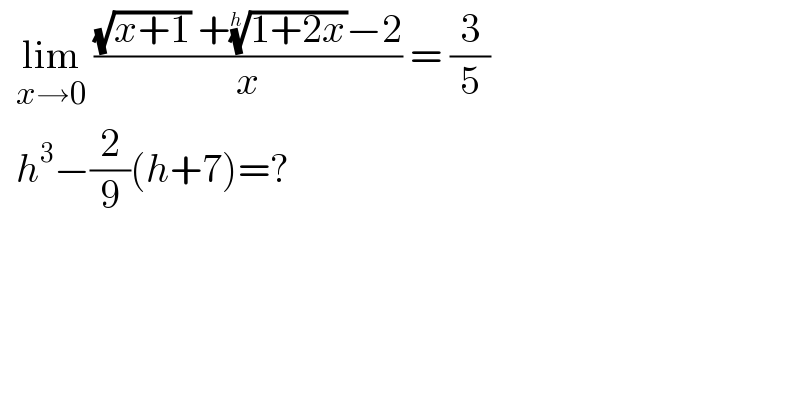
$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}+\mathrm{1}}\:+\sqrt[{{h}}]{\mathrm{1}+\mathrm{2}{x}}−\mathrm{2}}{{x}}\:=\:\frac{\mathrm{3}}{\mathrm{5}}\: \\ $$$$\:\:{h}^{\mathrm{3}} −\frac{\mathrm{2}}{\mathrm{9}}\left({h}+\mathrm{7}\right)=? \\ $$
Commented by vietanhdz last updated on 17/Dec/21
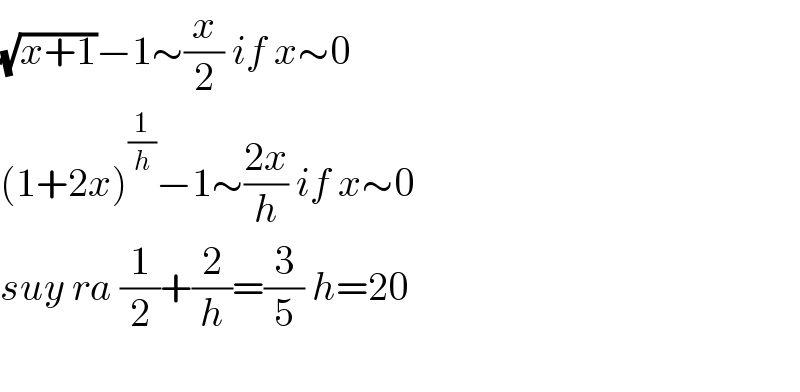
$$\sqrt{{x}+\mathrm{1}}−\mathrm{1}\sim\frac{{x}}{\mathrm{2}}\:{if}\:{x}\sim\mathrm{0} \\ $$$$\left(\mathrm{1}+\mathrm{2}{x}\right)^{\frac{\mathrm{1}}{{h}}} −\mathrm{1}\sim\frac{\mathrm{2}{x}}{{h}}\:{if}\:{x}\sim\mathrm{0} \\ $$$${suy}\:{ra}\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{{h}}=\frac{\mathrm{3}}{\mathrm{5}}\:{h}=\mathrm{20} \\ $$$$ \\ $$
