Question Number 125292 by Kurbanklichevs last updated on 09/Dec/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({x}+\mathrm{1}\right)^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)+{n}}{{x}^{\mathrm{2}} }\:\:\:\:\:{n}\in\mathbb{N} \\ $$$${Calculate}.\:\left({Without}\:{a}\:{L}'{Hopital}'{s}\:{rule}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 09/Dec/20
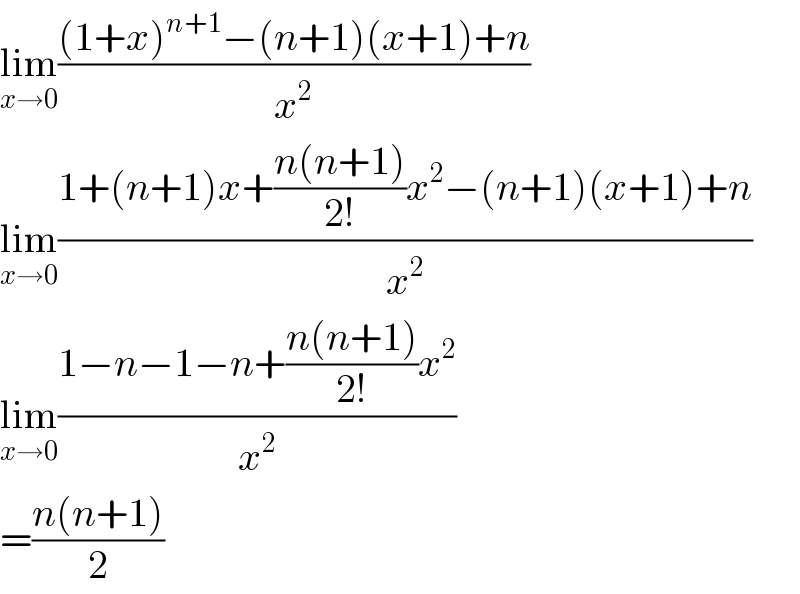
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)+{n}}{{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\left({n}+\mathrm{1}\right){x}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} −\left({n}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)+{n}}{{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−{n}−\mathrm{1}−{n}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$
Commented by Kurbanklichevs last updated on 10/Dec/20

$${Tank}\:{you} \\ $$
