Question Number 123813 by snipers237 last updated on 28/Nov/20
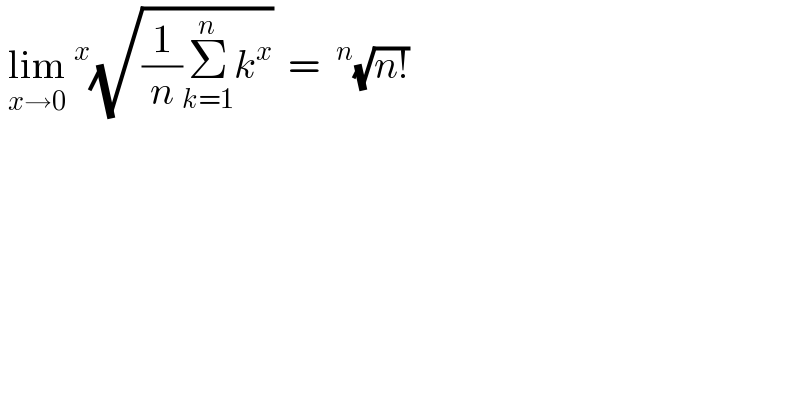
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:^{{x}} \sqrt{\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{{x}} }\:\:=\:\:^{{n}} \sqrt{{n}!}\: \\ $$
Answered by Dwaipayan Shikari last updated on 28/Nov/20
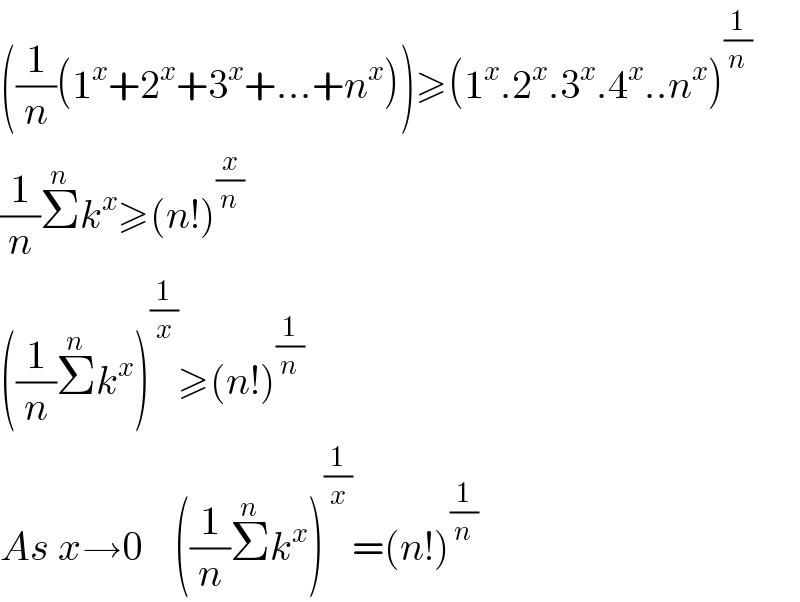
$$\left(\frac{\mathrm{1}}{{n}}\left(\mathrm{1}^{{x}} +\mathrm{2}^{{x}} +\mathrm{3}^{{x}} +…+{n}^{{x}} \right)\right)\geqslant\left(\mathrm{1}^{{x}} .\mathrm{2}^{{x}} .\mathrm{3}^{{x}} .\mathrm{4}^{{x}} ..{n}^{{x}} \right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\frac{\mathrm{1}}{{n}}\overset{{n}} {\sum}{k}^{{x}} \geqslant\left({n}!\right)^{\frac{{x}}{{n}}} \\ $$$$\left(\frac{\mathrm{1}}{{n}}\overset{{n}} {\sum}{k}^{{x}} \right)^{\frac{\mathrm{1}}{{x}}} \geqslant\left({n}!\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$${As}\:{x}\rightarrow\mathrm{0}\:\:\:\:\left(\frac{\mathrm{1}}{{n}}\overset{{n}} {\sum}{k}^{{x}} \right)^{\frac{\mathrm{1}}{{x}}} =\left({n}!\right)^{\frac{\mathrm{1}}{{n}}} \\ $$
