Question Number 104606 by john santu last updated on 22/Jul/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{{x}−\mathrm{1}}{\mid{x}−\mathrm{1}\mid}\:+\:\mid{x}\mid\right\}=? \\ $$
Answered by bobhans last updated on 22/Jul/20
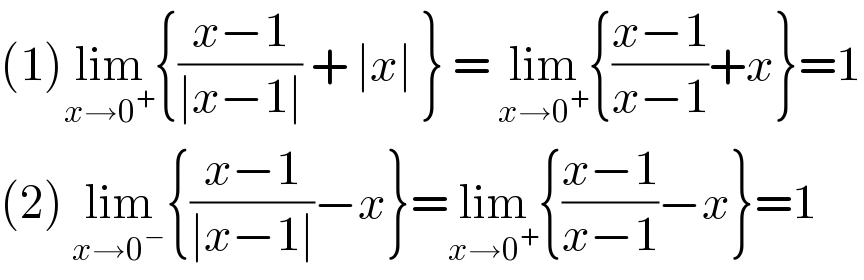
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left\{\frac{{x}−\mathrm{1}}{\mid{x}−\mathrm{1}\mid}\:+\:\mid{x}\mid\:\right\}\:=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left\{\frac{{x}−\mathrm{1}}{{x}−\mathrm{1}}+{x}\right\}=\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\left\{\frac{{x}−\mathrm{1}}{\mid{x}−\mathrm{1}\mid}−{x}\right\}=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left\{\frac{{x}−\mathrm{1}}{{x}−\mathrm{1}}−{x}\right\}=\mathrm{1} \\ $$
Answered by bramlex last updated on 22/Jul/20

