Question Number 58239 by salahahmed last updated on 20/Apr/19

$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left({x}^{\frac{\mathrm{1}}{{x}}} \right) \\ $$
Answered by salahahmed last updated on 23/Apr/19
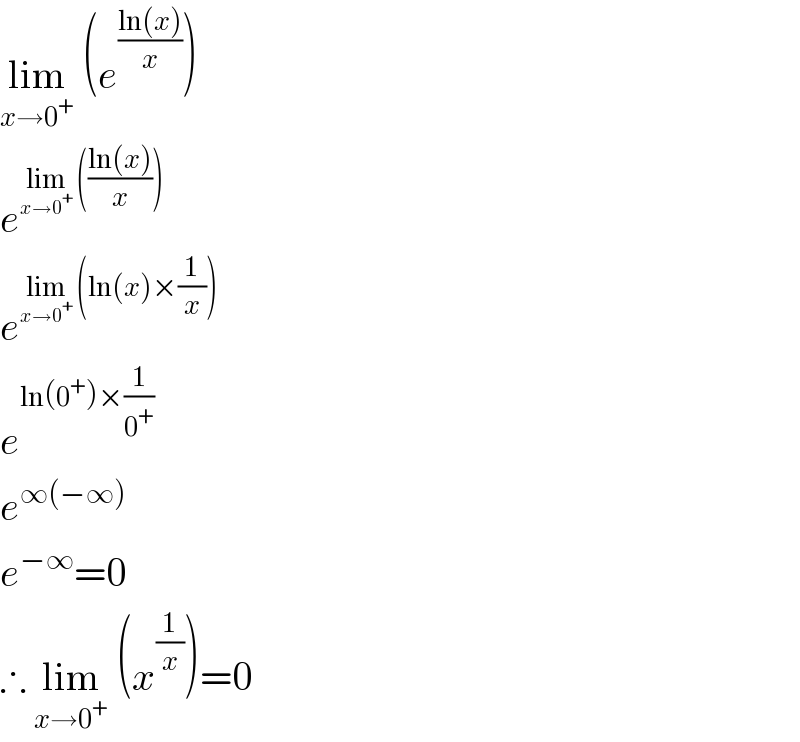
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left({e}^{\frac{\mathrm{ln}\left({x}\right)}{{x}}} \right) \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\frac{\mathrm{ln}\left({x}\right)}{{x}}\right)} \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\mathrm{ln}\left({x}\right)×\frac{\mathrm{1}}{{x}}\right)} \\ $$$${e}^{\mathrm{ln}\left(\mathrm{0}^{+} \right)×\frac{\mathrm{1}}{\mathrm{0}^{+} }} \\ $$$${e}^{\infty\left(−\infty\right)} \\ $$$${e}^{−\infty} =\mathrm{0} \\ $$$$\therefore\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left({x}^{\frac{\mathrm{1}}{{x}}} \right)=\mathrm{0} \\ $$
