Question Number 148848 by EDWIN88 last updated on 31/Jul/21
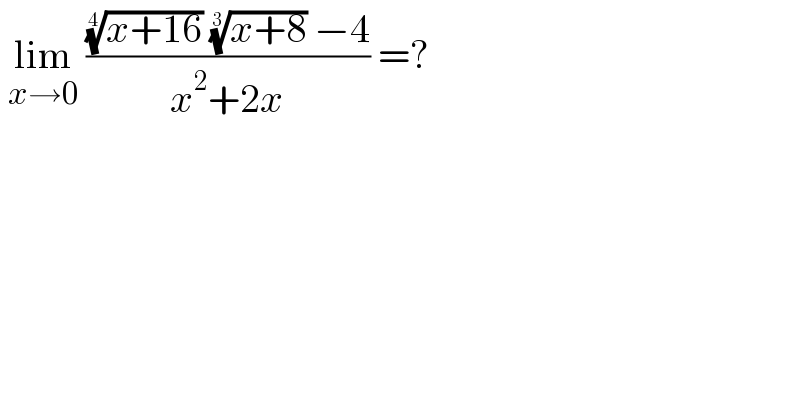
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{4}}]{{x}+\mathrm{16}}\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{8}}\:−\mathrm{4}}{{x}^{\mathrm{2}} +\mathrm{2}{x}}\:=?\: \\ $$
Answered by mathmax by abdo last updated on 01/Aug/21
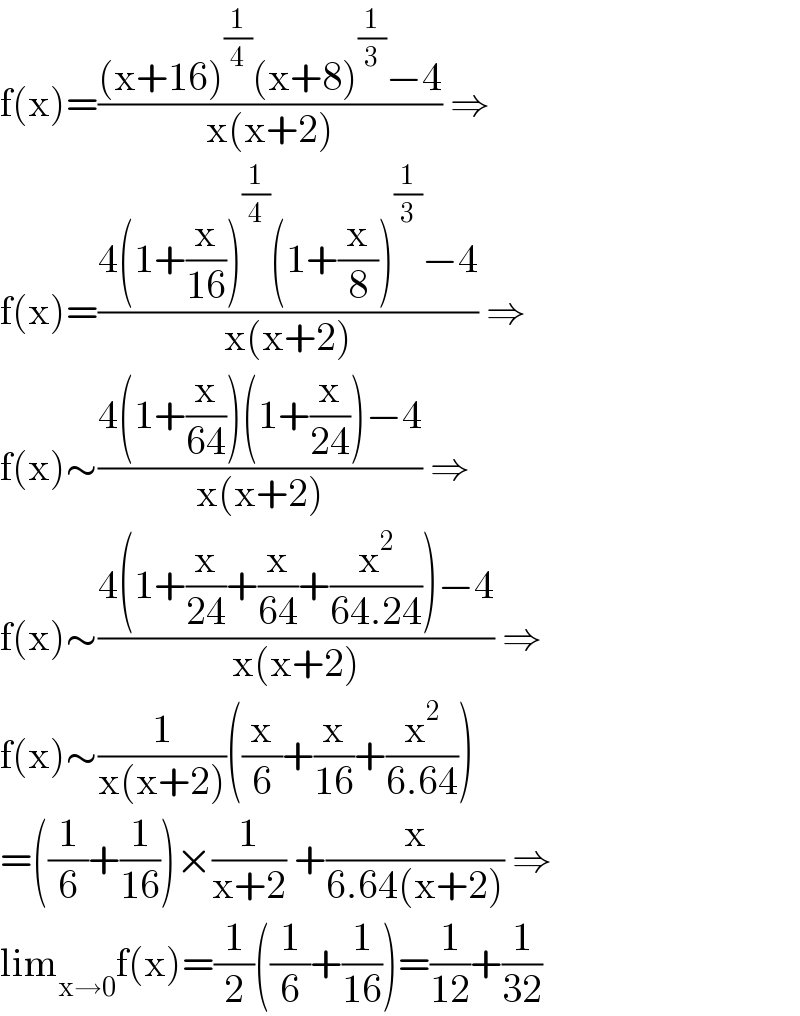
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\left(\mathrm{x}+\mathrm{16}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{x}+\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{4}}{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{4}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{16}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{8}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{4}}{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{4}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{64}}\right)\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{24}}\right)−\mathrm{4}}{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{4}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{24}}+\frac{\mathrm{x}}{\mathrm{64}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{64}.\mathrm{24}}\right)−\mathrm{4}}{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)}\left(\frac{\mathrm{x}}{\mathrm{6}}+\frac{\mathrm{x}}{\mathrm{16}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}.\mathrm{64}}\right) \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{16}}\right)×\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\:+\frac{\mathrm{x}}{\mathrm{6}.\mathrm{64}\left(\mathrm{x}+\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{16}}\right)=\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{32}} \\ $$
Answered by EDWIN88 last updated on 01/Aug/21
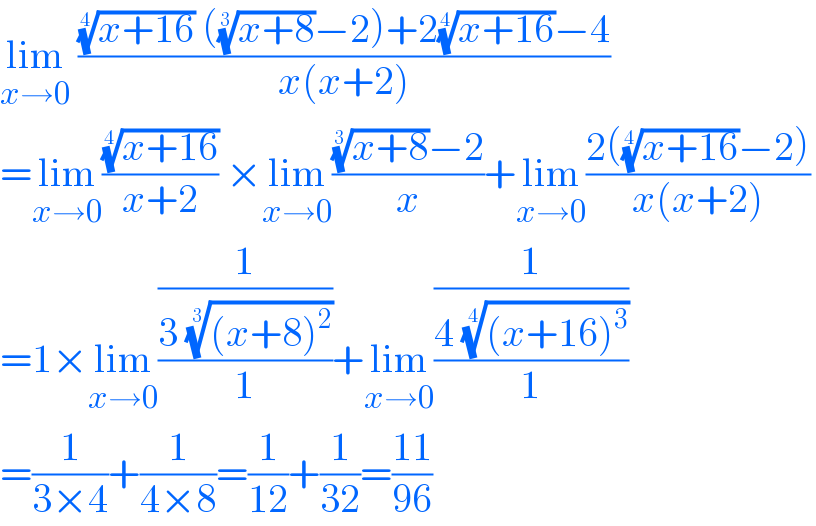
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{4}}]{{x}+\mathrm{16}}\:\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{8}}−\mathrm{2}\right)+\mathrm{2}\sqrt[{\mathrm{4}}]{{x}+\mathrm{16}}−\mathrm{4}}{{x}\left({x}+\mathrm{2}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{4}}]{{x}+\mathrm{16}}}{{x}+\mathrm{2}}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{{x}+\mathrm{8}}−\mathrm{2}}{{x}}+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left(\sqrt[{\mathrm{4}}]{{x}+\mathrm{16}}−\mathrm{2}\right)}{{x}\left({x}+\mathrm{2}\right)} \\ $$$$=\mathrm{1}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{3}\:\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{8}\right)^{\mathrm{2}} }}}{\mathrm{1}}+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{4}\:\sqrt[{\mathrm{4}}]{\left({x}+\mathrm{16}\right)^{\mathrm{3}} }}}{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}×\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}×\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{32}}=\frac{\mathrm{11}}{\mathrm{96}}\: \\ $$
