Question Number 161111 by cortano last updated on 12/Dec/21
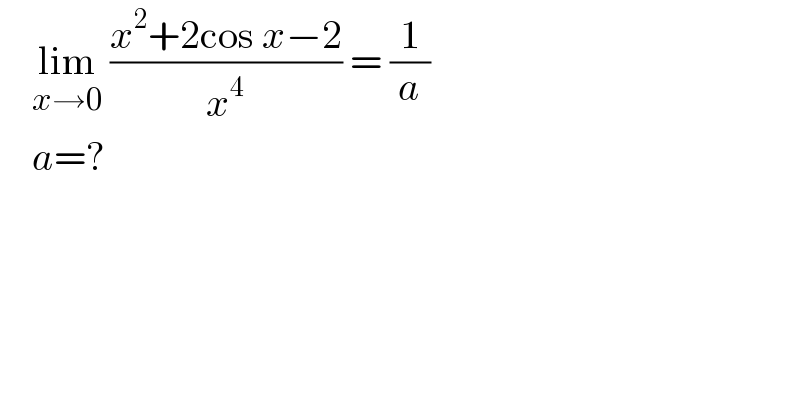
$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} +\mathrm{2cos}\:{x}−\mathrm{2}}{{x}^{\mathrm{4}} }\:=\:\frac{\mathrm{1}}{{a}} \\ $$$$\:\:\:\:{a}=? \\ $$
Commented by blackmamba last updated on 12/Dec/21
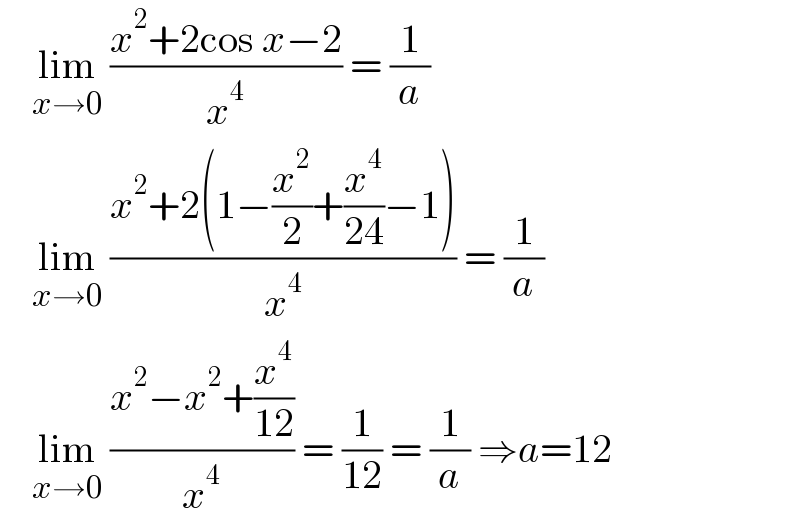
$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} +\mathrm{2cos}\:{x}−\mathrm{2}}{{x}^{\mathrm{4}} }\:=\:\frac{\mathrm{1}}{{a}} \\ $$$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{4}} }{\mathrm{24}}−\mathrm{1}\right)}{{x}^{\mathrm{4}} }\:=\:\frac{\mathrm{1}}{{a}} \\ $$$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{12}}}{{x}^{\mathrm{4}} }\:=\:\frac{\mathrm{1}}{\mathrm{12}}\:=\:\frac{\mathrm{1}}{{a}}\:\Rightarrow{a}=\mathrm{12} \\ $$
Answered by yeti123 last updated on 12/Dec/21
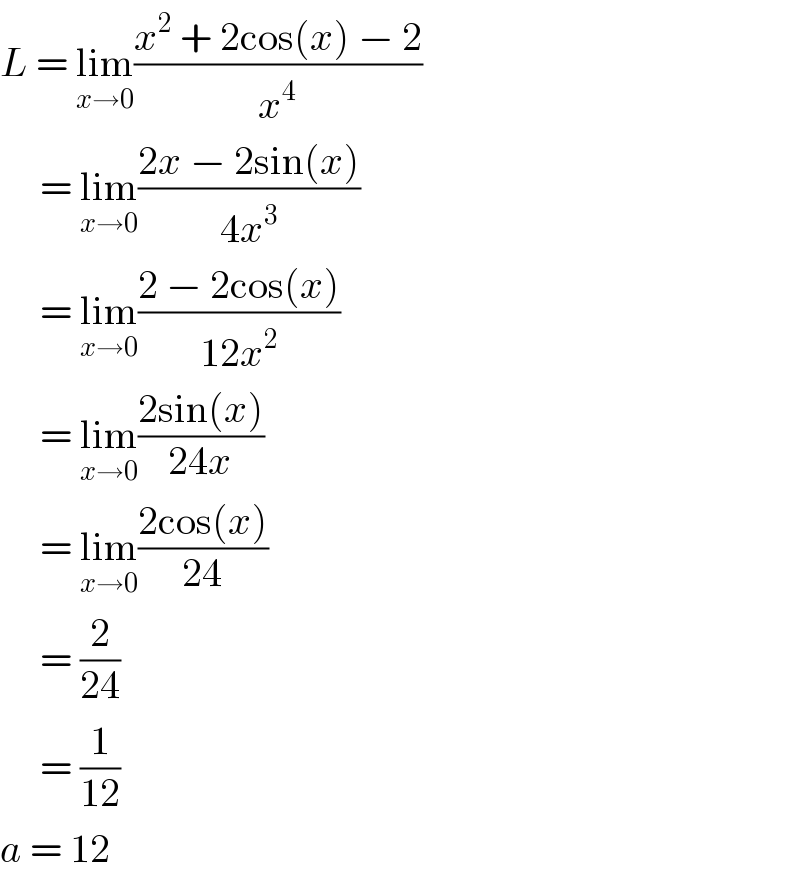
$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} \:+\:\mathrm{2cos}\left({x}\right)\:−\:\mathrm{2}}{{x}^{\mathrm{4}} } \\ $$$$\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}{x}\:−\:\mathrm{2sin}\left({x}\right)}{\mathrm{4}{x}^{\mathrm{3}} } \\ $$$$\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\:−\:\mathrm{2cos}\left({x}\right)}{\mathrm{12}{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\left({x}\right)}{\mathrm{24}{x}} \\ $$$$\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2cos}\left({x}\right)}{\mathrm{24}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{2}}{\mathrm{24}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${a}\:=\:\mathrm{12} \\ $$
