Question Number 119482 by liberty last updated on 24/Oct/20
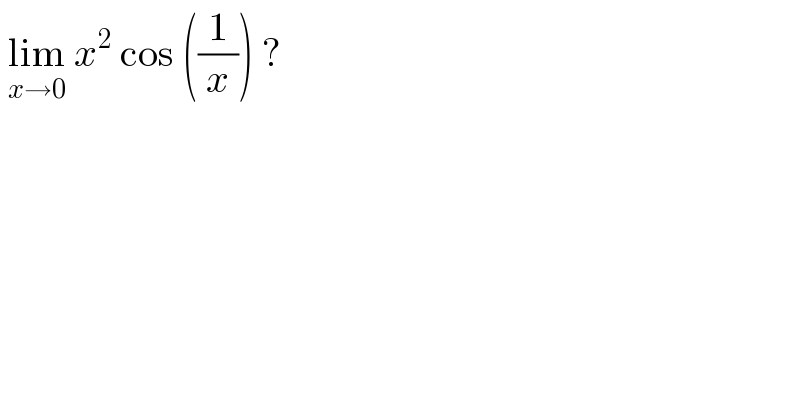
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\:? \\ $$
Answered by Olaf last updated on 25/Oct/20
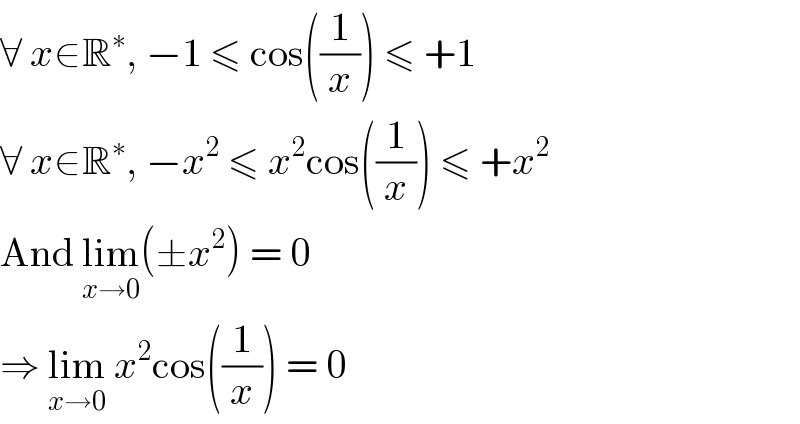
$$\forall\:{x}\in\mathbb{R}^{\ast} ,\:−\mathrm{1}\:\leqslant\:\mathrm{cos}\left(\frac{\mathrm{1}}{{x}}\right)\:\leqslant\:+\mathrm{1} \\ $$$$\forall\:{x}\in\mathbb{R}^{\ast} ,\:−{x}^{\mathrm{2}} \:\leqslant\:{x}^{\mathrm{2}} \mathrm{cos}\left(\frac{\mathrm{1}}{{x}}\right)\:\leqslant\:+{x}^{\mathrm{2}} \\ $$$$\mathrm{And}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\pm{x}^{\mathrm{2}} \right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{\mathrm{2}} \mathrm{cos}\left(\frac{\mathrm{1}}{{x}}\right)\:=\:\mathrm{0} \\ $$
