Menu Close

lim-x-0-x-2-tan-1-x-3-0-x-sin-t-2-dt-x-5-

Tinku Tara 0 Comments
Pin




Question Number 56202 by naka3546 last updated on 12/Mar/19
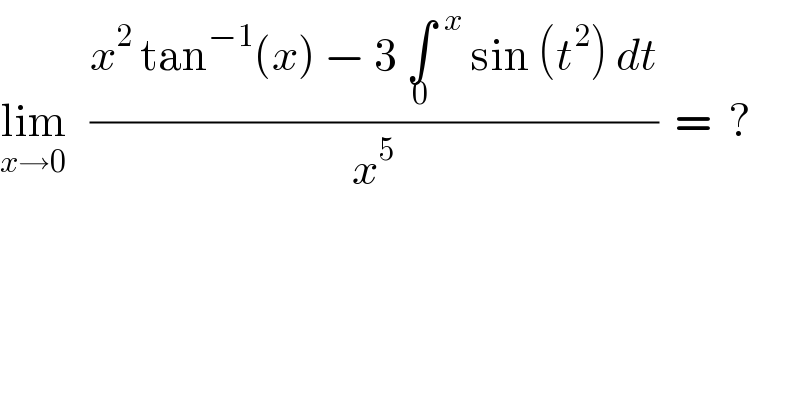
lim_(x→0) ((x^2 tan^(−1) (x) − 3 ∫_0 ^x sin (t^2 ) dt)/x^5 ) = ?
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{{x}^{\mathrm{2}} \:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\:−\:\mathrm{3}\:\underset{\mathrm{0}} {\int}\:\overset{{x}} {\:}\:\mathrm{sin}\:\left({t}^{\mathrm{2}} \right)\:{dt}}{{x}^{\mathrm{5}} }\:\:=\:\:? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Mar/19
g(x)=∫_0 ^x sin(t^2 )dt (dg/dx)=∫_0 ^x (∂/∂x)(sint^2 )dt +sinx^2 ×(dx/dx) −sin0^2 ×((d(0))/dx) =sinx^2 lim_(x→0) ((x^2 ×(1/(1+x^2 ))+2xtan^(−1) (x)−3sinx^2 )/(5x^4 ))((0/0))form lim_(x→0) (((((1+x^2 )2x−x^2 (2x))/((1+x^2 )^2 ))+((2x)/(1+x^2 ))+2tan^(−1) (x)−6xcosx^2 )/(20x^3 )) lim_(x→0) ((((2x)/((1+x^2 )^2 ))+((2x)/(1+x^2 ))+2tan^(−1) (x)−6xcosx^2 )/(20x^3 ))((0/0)) lim_(x→0) ((2x+2x+2x^3 +2tan^(−1) (x)×(1+x^2 )^2 −6x(1+x^2 )^2 cosx^2 )/(20x^3 (1+x^2 )^2 )) wait...complicated ...still to differntiate...for LH rule...
$${g}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} {sin}\left({t}^{\mathrm{2}} \right){dt} \\ $$$$\frac{{dg}}{{dx}}=\int_{\mathrm{0}} ^{{x}} \frac{\partial}{\partial{x}}\left({sint}^{\mathrm{2}} \right){dt}\:+{sinx}^{\mathrm{2}} ×\frac{{dx}}{{dx}}\:−{sin}\mathrm{0}^{\mathrm{2}} ×\frac{{d}\left(\mathrm{0}\right)}{{dx}} \\ $$$$={sinx}^{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{2}{xtan}^{−\mathrm{1}} \left({x}\right)−\mathrm{3}{sinx}^{\mathrm{2}} }{\mathrm{5}{x}^{\mathrm{4}} }\left(\frac{\mathrm{0}}{\mathrm{0}}\right){form} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mathrm{2}{x}−{x}^{\mathrm{2}} \left(\mathrm{2}{x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{2}{tan}^{−\mathrm{1}} \left({x}\right)−\mathrm{6}{xcosx}^{\mathrm{2}} }{\mathrm{20}{x}^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\frac{\mathrm{2}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{2}{tan}^{−\mathrm{1}} \left({x}\right)−\mathrm{6}{xcosx}^{\mathrm{2}} }{\mathrm{20}{x}^{\mathrm{3}} }\left(\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{2}{x}+\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{3}} +\mathrm{2}{tan}^{−\mathrm{1}} \left({x}\right)×\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{6}{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} {cosx}^{\mathrm{2}} }{\mathrm{20}{x}^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${wait}…{complicated}\:…{still}\:{to}\:{differntiate}…{for}\:{LH} \\ $$$${rule}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *