Question Number 90226 by manuel__ last updated on 22/Apr/20
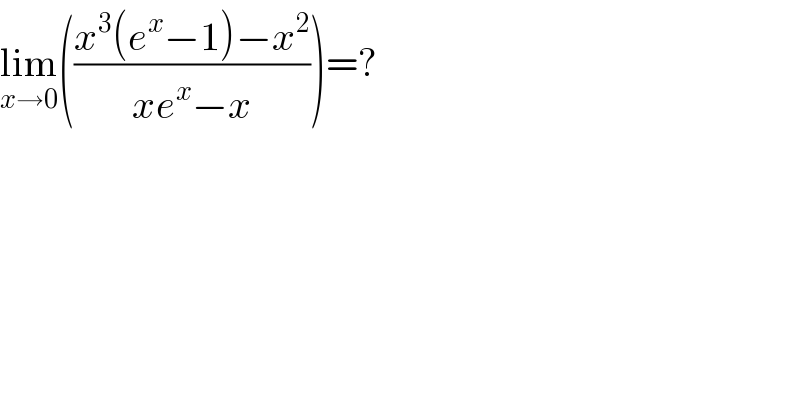
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}^{\mathrm{3}} \left({e}^{{x}} −\mathrm{1}\right)−{x}^{\mathrm{2}} }{{xe}^{{x}} −{x}}\right)=? \\ $$
Commented by john santu last updated on 22/Apr/20
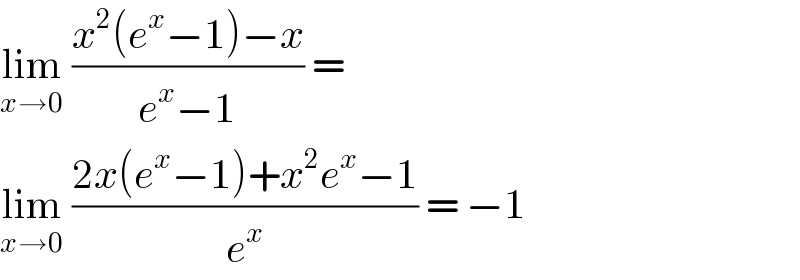
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \left({e}^{{x}} −\mathrm{1}\right)−{x}}{{e}^{{x}} −\mathrm{1}}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}\left({e}^{{x}} −\mathrm{1}\right)+{x}^{\mathrm{2}} {e}^{{x}} −\mathrm{1}}{{e}^{{x}} }\:=\:−\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 22/Apr/20
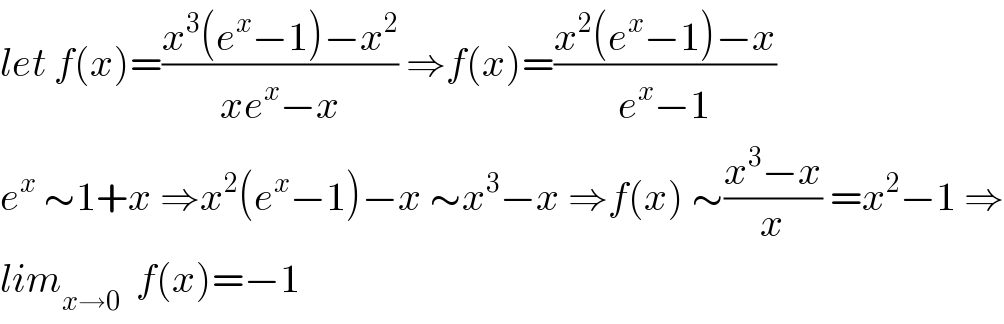
$${let}\:{f}\left({x}\right)=\frac{{x}^{\mathrm{3}} \left({e}^{{x}} −\mathrm{1}\right)−{x}^{\mathrm{2}} }{{xe}^{{x}} −{x}}\:\Rightarrow{f}\left({x}\right)=\frac{{x}^{\mathrm{2}} \left({e}^{{x}} −\mathrm{1}\right)−{x}}{{e}^{{x}} −\mathrm{1}} \\ $$$${e}^{{x}} \:\sim\mathrm{1}+{x}\:\Rightarrow{x}^{\mathrm{2}} \left({e}^{{x}} −\mathrm{1}\right)−{x}\:\sim{x}^{\mathrm{3}} −{x}\:\Rightarrow{f}\left({x}\right)\:\sim\frac{{x}^{\mathrm{3}} −{x}}{{x}}\:={x}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)=−\mathrm{1} \\ $$
