Question Number 127846 by bemath last updated on 02/Jan/21
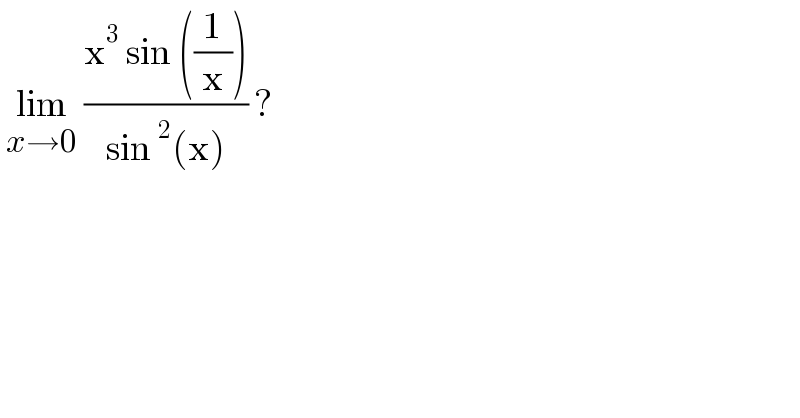
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{3}} \:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{x}\right)}\:?\: \\ $$
Commented by Dwaipayan Shikari last updated on 02/Jan/21
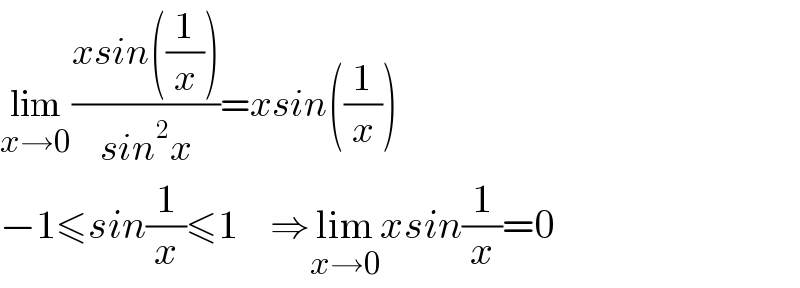
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{xsin}\left(\frac{\mathrm{1}}{{x}}\right)}{{sin}^{\mathrm{2}} {x}}={xsin}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$$−\mathrm{1}\leqslant{sin}\frac{\mathrm{1}}{{x}}\leqslant\mathrm{1}\:\:\:\:\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{xsin}\frac{\mathrm{1}}{{x}}=\mathrm{0} \\ $$
