Question Number 101366 by bobhans last updated on 02/Jul/20
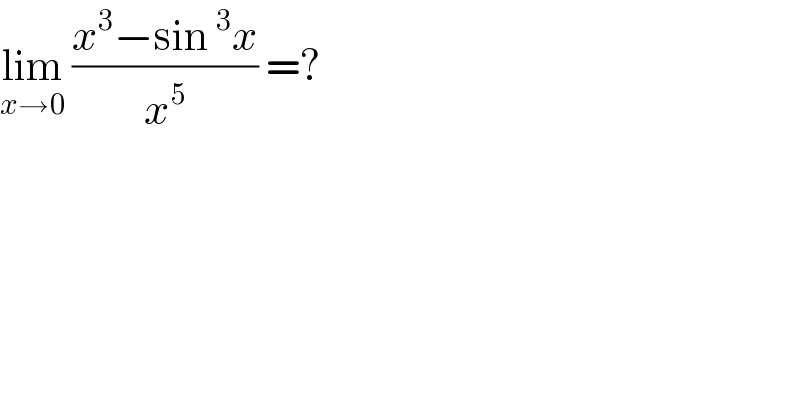
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} −\mathrm{sin}\:^{\mathrm{3}} {x}}{{x}^{\mathrm{5}} }\:=? \\ $$
Commented by Dwaipayan Shikari last updated on 02/Jul/20
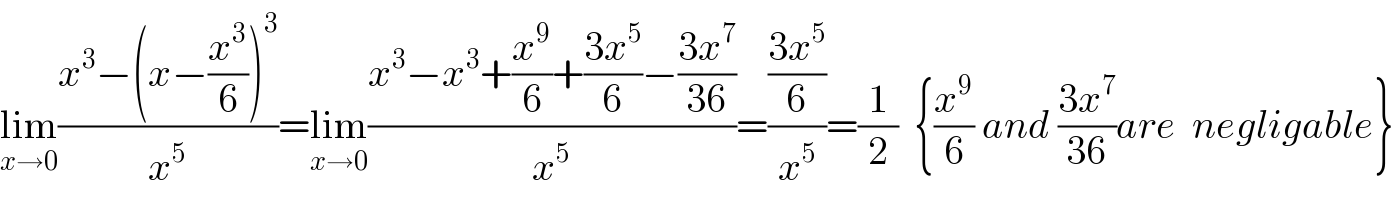
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} −\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)^{\mathrm{3}} }{{x}^{\mathrm{5}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{3}} −{x}^{\mathrm{3}} +\frac{{x}^{\mathrm{9}} }{\mathrm{6}}+\frac{\mathrm{3}{x}^{\mathrm{5}} }{\mathrm{6}}−\frac{\mathrm{3}{x}^{\mathrm{7}} }{\mathrm{36}}}{{x}^{\mathrm{5}} }=\frac{\frac{\mathrm{3}{x}^{\mathrm{5}} }{\mathrm{6}}}{{x}^{\mathrm{5}} }=\frac{\mathrm{1}}{\mathrm{2}}\:\:\left\{\frac{{x}^{\mathrm{9}} }{\mathrm{6}}\:{and}\:\frac{\mathrm{3}{x}^{\mathrm{7}} }{\mathrm{36}}{are}\:\:{negligable}\right\} \\ $$
Commented by bemath last updated on 02/Jul/20

$$\mathrm{agree} \\ $$
Answered by ajfour last updated on 02/Jul/20
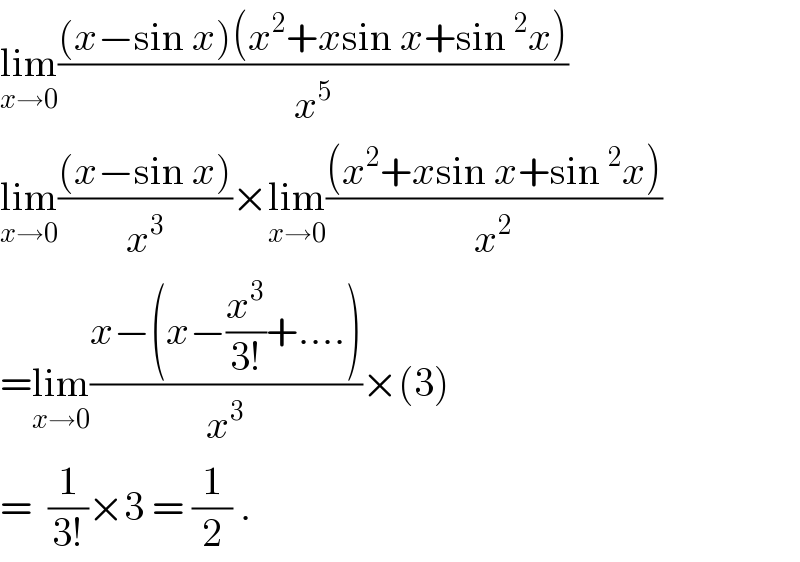
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}−\mathrm{sin}\:{x}\right)\left({x}^{\mathrm{2}} +{x}\mathrm{sin}\:{x}+\mathrm{sin}\:^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{5}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}−\mathrm{sin}\:{x}\right)}{{x}^{\mathrm{3}} }×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}^{\mathrm{2}} +{x}\mathrm{sin}\:{x}+\mathrm{sin}\:^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+….\right)}{{x}^{\mathrm{3}} }×\left(\mathrm{3}\right) \\ $$$$=\:\:\frac{\mathrm{1}}{\mathrm{3}!}×\mathrm{3}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
Commented by bemath last updated on 02/Jul/20
$$\mathrm{yes}..\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
