Question Number 99244 by Ar Brandon last updated on 19/Jun/20
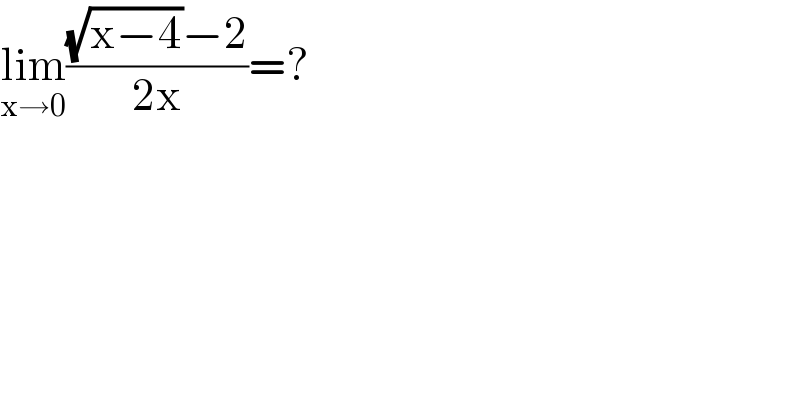
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{x}−\mathrm{4}}−\mathrm{2}}{\mathrm{2x}}=? \\ $$
Answered by mahdi last updated on 19/Jun/20
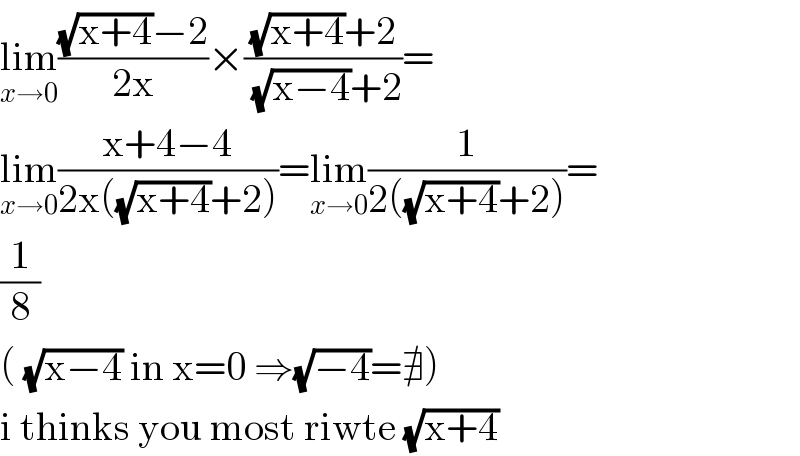
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{x}+\mathrm{4}}−\mathrm{2}}{\mathrm{2x}}×\frac{\sqrt{\mathrm{x}+\mathrm{4}}+\mathrm{2}}{\:\sqrt{\mathrm{x}−\mathrm{4}}+\mathrm{2}}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}+\mathrm{4}−\mathrm{4}}{\mathrm{2x}\left(\sqrt{\mathrm{x}+\mathrm{4}}+\mathrm{2}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}\left(\sqrt{\mathrm{x}+\mathrm{4}}+\mathrm{2}\right)}= \\ $$$$\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\left(\:\sqrt{\mathrm{x}−\mathrm{4}}\:\mathrm{in}\:\mathrm{x}=\mathrm{0}\:\Rightarrow\sqrt{−\mathrm{4}}=\nexists\right) \\ $$$$\mathrm{i}\:\mathrm{thinks}\:\mathrm{you}\:\mathrm{most}\:\mathrm{riwte}\:\sqrt{\mathrm{x}+\mathrm{4}} \\ $$
Commented by Aziztisffola last updated on 19/Jun/20

$$=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Commented by Ar Brandon last updated on 19/Jun/20
If it was the case I wouldn't have had problems. I also felt it's been erred.��
Commented by mahdi last updated on 19/Jun/20
$$\left.\mathrm{tanks}\:\mathrm{Aziztisffola}\:\mathrm{for}\:\mathrm{giude}\::\right) \\ $$
