Question Number 118966 by bramlexs22 last updated on 21/Oct/20

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}+{bx}^{\mathrm{2}} }−\sqrt{{x}}}{{bx}\sqrt{{x}}}\:=? \\ $$
Answered by benjo_mathlover last updated on 21/Oct/20
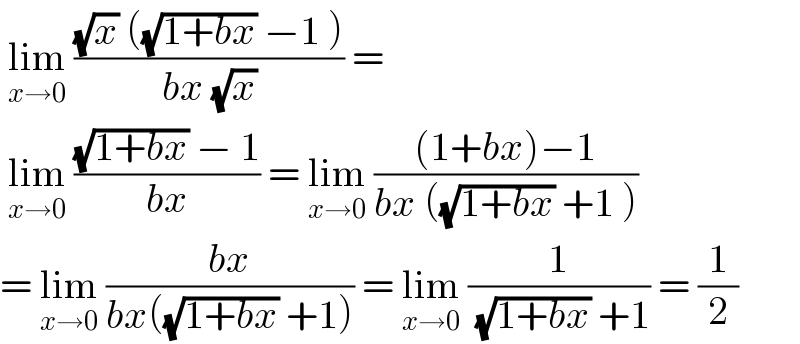
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}}\:\left(\sqrt{\mathrm{1}+{bx}}\:−\mathrm{1}\:\right)}{{bx}\:\sqrt{{x}}}\:=\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+{bx}}\:−\:\mathrm{1}}{{bx}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+{bx}\right)−\mathrm{1}}{{bx}\:\left(\sqrt{\mathrm{1}+{bx}}\:+\mathrm{1}\:\right)} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{bx}}{{bx}\left(\sqrt{\mathrm{1}+{bx}}\:+\mathrm{1}\right)}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{bx}}\:+\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
