Question Number 153039 by ZiYangLee last updated on 04/Sep/21
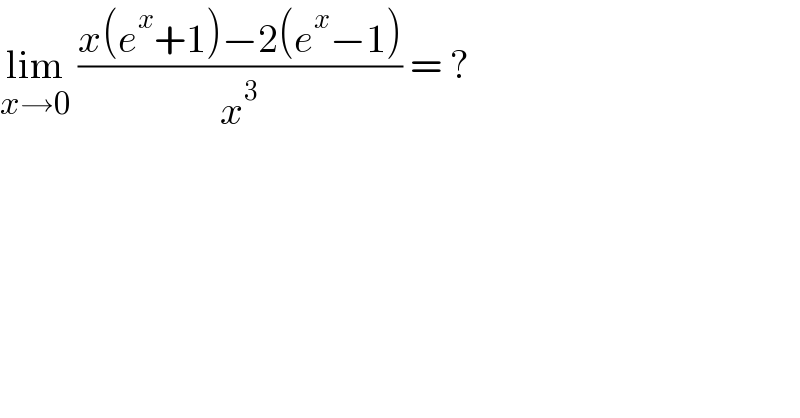
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left({e}^{{x}} +\mathrm{1}\right)−\mathrm{2}\left({e}^{{x}} −\mathrm{1}\right)}{{x}^{\mathrm{3}} }\:=\:? \\ $$
Answered by puissant last updated on 04/Sep/21
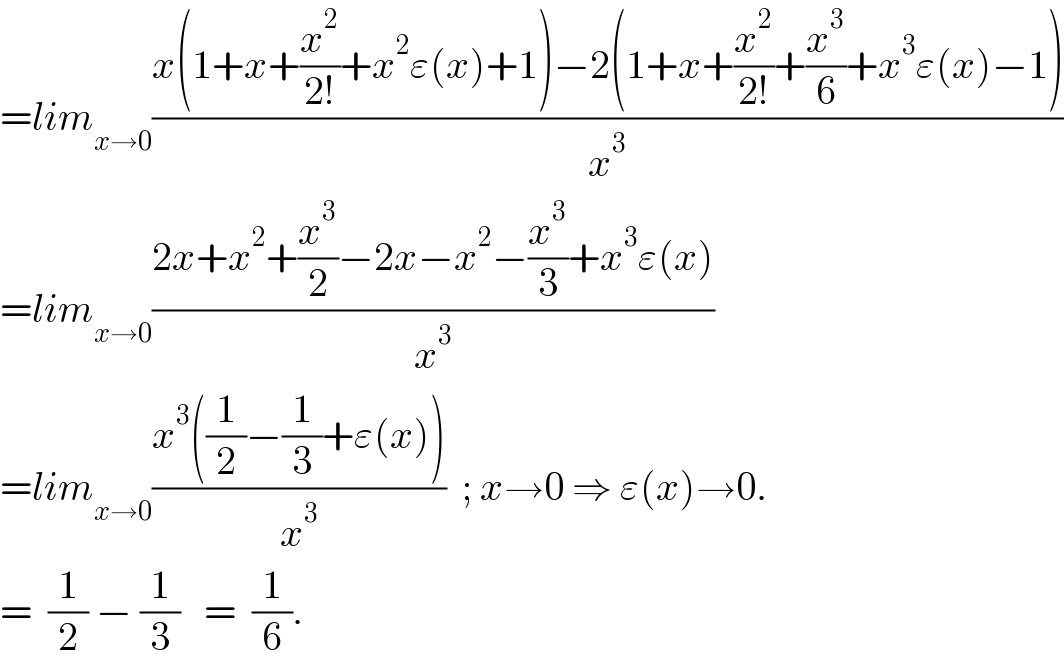
$$={lim}_{{x}\rightarrow\mathrm{0}} \frac{{x}\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+{x}^{\mathrm{2}} \varepsilon\left({x}\right)+\mathrm{1}\right)−\mathrm{2}\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{x}^{\mathrm{3}} \varepsilon\left({x}\right)−\mathrm{1}\right)}{{x}^{\mathrm{3}} } \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{2}{x}+{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{3}} }{\mathrm{2}}−\mathrm{2}{x}−{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+{x}^{\mathrm{3}} \varepsilon\left({x}\right)}{{x}^{\mathrm{3}} } \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \frac{{x}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\varepsilon\left({x}\right)\right)}{{x}^{\mathrm{3}} }\:\:;\:{x}\rightarrow\mathrm{0}\:\Rightarrow\:\varepsilon\left({x}\right)\rightarrow\mathrm{0}. \\ $$$$=\:\:\frac{\mathrm{1}}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{6}}. \\ $$
