Question Number 85625 by jagoll last updated on 23/Mar/20
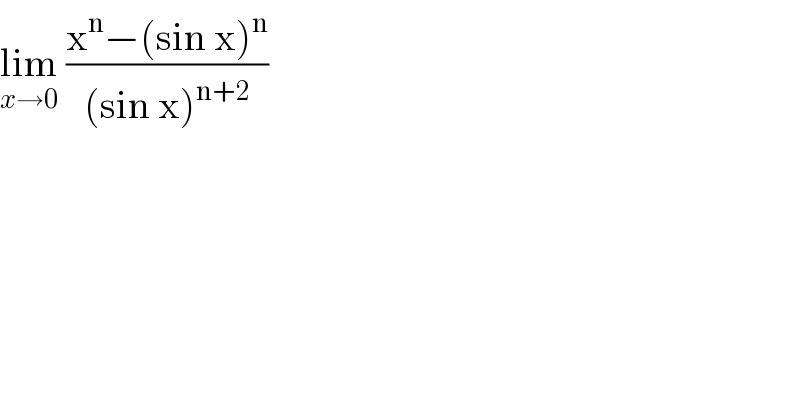
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{n}} −\left(\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{n}} }{\left(\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{n}+\mathrm{2}} } \\ $$
Answered by john santu last updated on 23/Mar/20
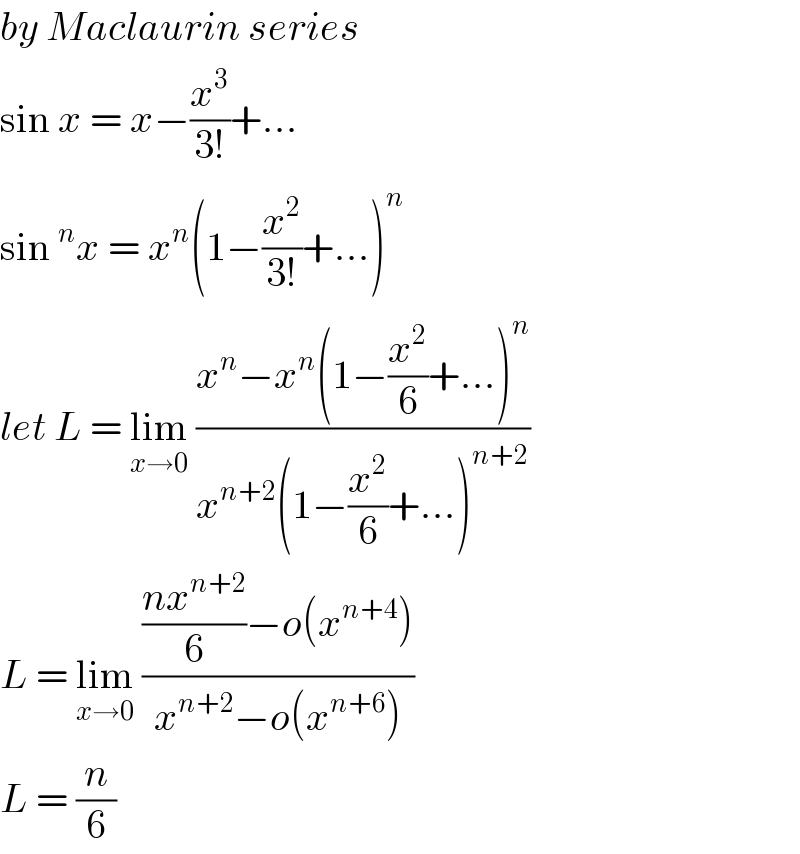
$${by}\:{Maclaurin}\:{series} \\ $$$$\mathrm{sin}\:{x}\:=\:{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+… \\ $$$$\mathrm{sin}\:^{{n}} {x}\:=\:{x}^{{n}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}!}+…\right)^{{n}} \\ $$$${let}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{{n}} −{x}^{{n}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+…\right)^{{n}} }{{x}^{{n}+\mathrm{2}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+…\right)^{{n}+\mathrm{2}} } \\ $$$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{nx}^{{n}+\mathrm{2}} }{\mathrm{6}}−{o}\left({x}^{{n}+\mathrm{4}} \right)}{{x}^{{n}+\mathrm{2}} −{o}\left({x}^{{n}+\mathrm{6}} \right)} \\ $$$${L}\:=\:\frac{{n}}{\mathrm{6}} \\ $$
