Question Number 90944 by john santu last updated on 27/Apr/20
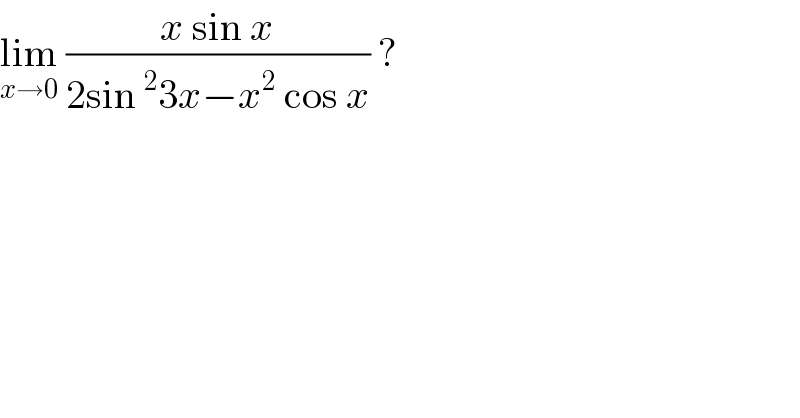
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\:\mathrm{sin}\:{x}}{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{3}{x}−{x}^{\mathrm{2}} \:\mathrm{cos}\:{x}}\:? \\ $$
Commented by john santu last updated on 27/Apr/20

Commented by mathmax by abdo last updated on 27/Apr/20
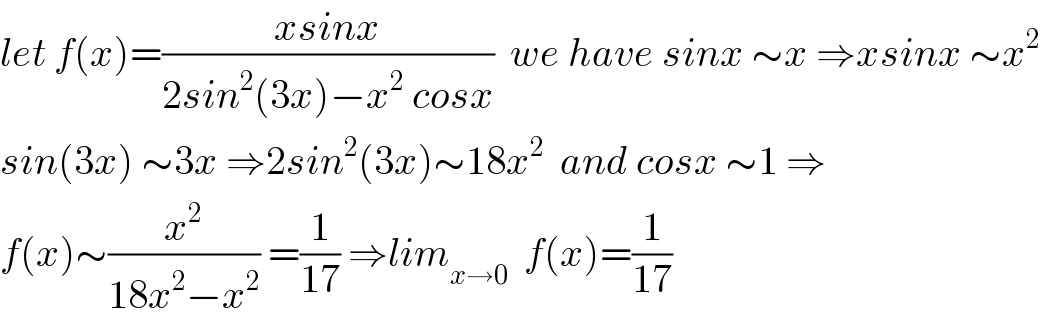
$${let}\:{f}\left({x}\right)=\frac{{xsinx}}{\mathrm{2}{sin}^{\mathrm{2}} \left(\mathrm{3}{x}\right)−{x}^{\mathrm{2}} \:{cosx}}\:\:{we}\:{have}\:{sinx}\:\sim{x}\:\Rightarrow{xsinx}\:\sim{x}^{\mathrm{2}} \\ $$$${sin}\left(\mathrm{3}{x}\right)\:\sim\mathrm{3}{x}\:\Rightarrow\mathrm{2}{sin}^{\mathrm{2}} \left(\mathrm{3}{x}\right)\sim\mathrm{18}{x}^{\mathrm{2}} \:\:{and}\:{cosx}\:\sim\mathrm{1}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{{x}^{\mathrm{2}} }{\mathrm{18}{x}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{17}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{17}} \\ $$
Commented by john santu last updated on 27/Apr/20

$$\mathrm{good}\:\mathrm{sir}\: \\ $$
