Question Number 118681 by bemath last updated on 19/Oct/20
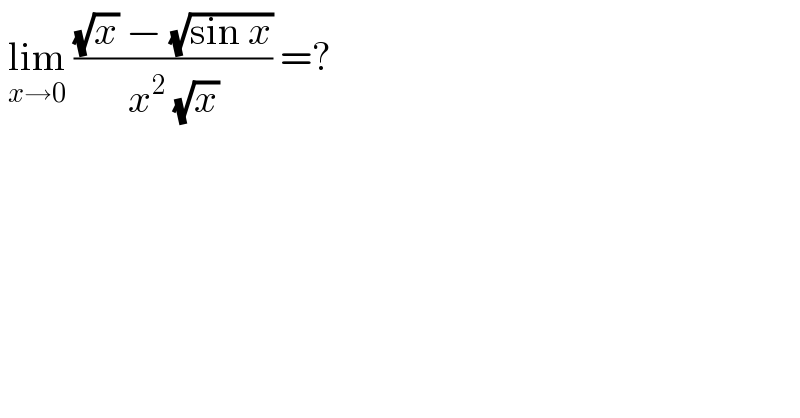
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}}\:−\:\sqrt{\mathrm{sin}\:{x}}}{{x}^{\mathrm{2}} \:\sqrt{{x}}}\:=? \\ $$
Answered by benjo_mathlover last updated on 19/Oct/20
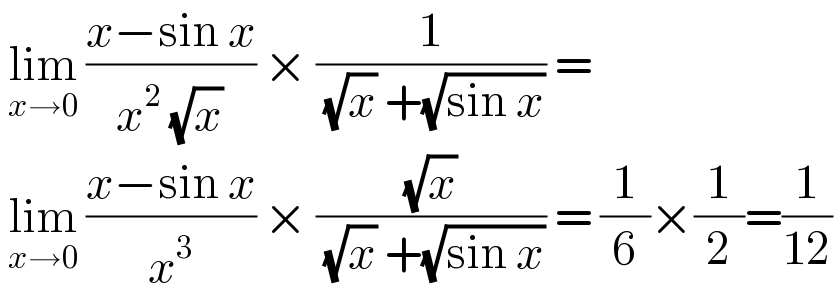
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} \:\sqrt{{x}}}\:×\:\frac{\mathrm{1}}{\:\sqrt{{x}}\:+\sqrt{\mathrm{sin}\:{x}}}\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{3}} }\:×\:\frac{\sqrt{{x}}}{\:\sqrt{{x}}\:+\sqrt{\mathrm{sin}\:{x}}}\:=\:\frac{\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$
Commented by Lordose last updated on 19/Oct/20

$$\mathrm{Very}\:\mathrm{correct} \\ $$
Commented by 1549442205PVT last updated on 19/Oct/20
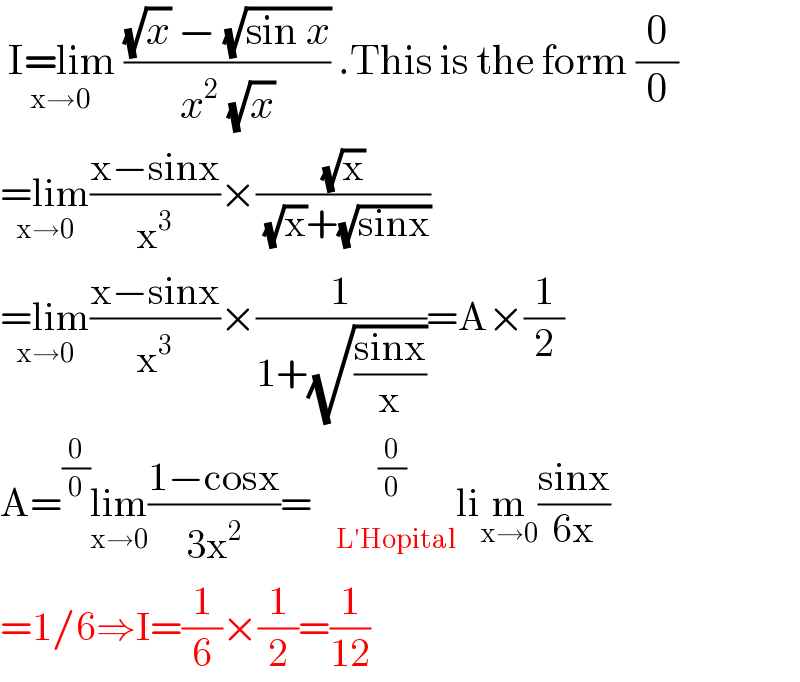
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\:\mathrm{I}=\mathrm{lim}\:}\frac{\sqrt{{x}}\:−\:\sqrt{\mathrm{sin}\:{x}}}{{x}^{\mathrm{2}} \:\sqrt{{x}}}\:.\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{form}\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {=\mathrm{lim}}\frac{\mathrm{x}−\mathrm{sinx}}{\mathrm{x}^{\mathrm{3}} }×\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}}+\sqrt{\mathrm{sinx}}} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {=\mathrm{lim}}\frac{\mathrm{x}−\mathrm{sinx}}{\mathrm{x}^{\mathrm{3}} }×\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\frac{\mathrm{sinx}}{\mathrm{x}}}}=\mathrm{A}×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{A}=^{\frac{\mathrm{0}}{\mathrm{0}}} \underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{3x}^{\mathrm{2}} }=\:\:\:\underset{\mathrm{L}'\mathrm{Hopital}} {\:\:^{\frac{\mathrm{0}}{\mathrm{0}}} \:\:\:}\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\mathrm{sinx}}{\mathrm{6x}} \\ $$$$=\mathrm{1}/\mathrm{6}\Rightarrow\mathrm{I}=\frac{\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$
Answered by mathmax by abdo last updated on 19/Oct/20
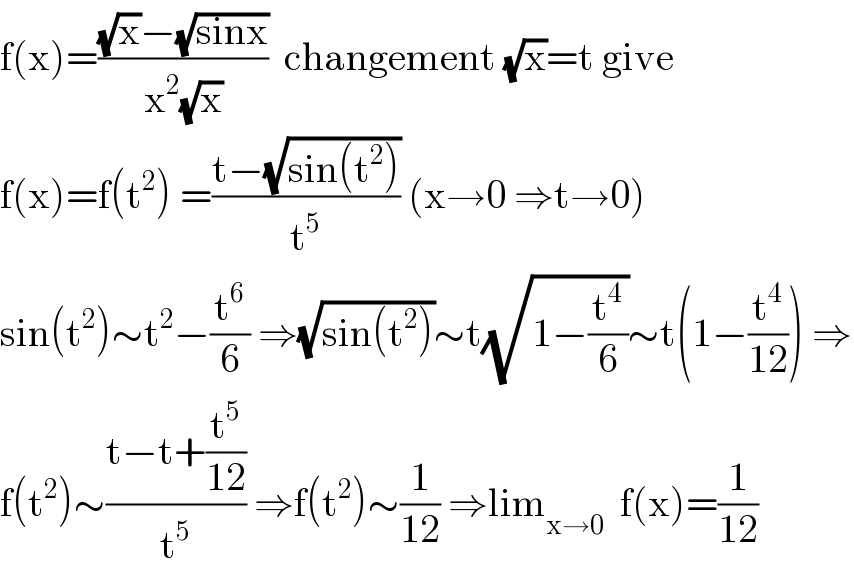
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{x}}−\sqrt{\mathrm{sinx}}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}}}\:\:\mathrm{changement}\:\sqrt{\mathrm{x}}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{t}^{\mathrm{2}} \right)\:=\frac{\mathrm{t}−\sqrt{\mathrm{sin}\left(\mathrm{t}^{\mathrm{2}} \right)}}{\mathrm{t}^{\mathrm{5}} }\:\left(\mathrm{x}\rightarrow\mathrm{0}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\right)\: \\ $$$$\mathrm{sin}\left(\mathrm{t}^{\mathrm{2}} \right)\sim\mathrm{t}^{\mathrm{2}} −\frac{\mathrm{t}^{\mathrm{6}} }{\mathrm{6}}\:\Rightarrow\sqrt{\mathrm{sin}\left(\mathrm{t}^{\mathrm{2}} \right)}\sim\mathrm{t}\sqrt{\mathrm{1}−\frac{\mathrm{t}^{\mathrm{4}} }{\mathrm{6}}}\sim\mathrm{t}\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{4}} }{\mathrm{12}}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{t}^{\mathrm{2}} \right)\sim\frac{\mathrm{t}−\mathrm{t}+\frac{\mathrm{t}^{\mathrm{5}} }{\mathrm{12}}}{\mathrm{t}^{\mathrm{5}} }\:\Rightarrow\mathrm{f}\left(\mathrm{t}^{\mathrm{2}} \right)\sim\frac{\mathrm{1}}{\mathrm{12}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{12}} \\ $$
