Question Number 18587 by Joel577 last updated on 25/Jul/17

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\:.\:\mathrm{tan}\:{x}}{{x}\:\mathrm{sin}\:{x}\:−\:\mathrm{cos}\:{x}\:+\:\mathrm{1}} \\ $$
Commented by Joel577 last updated on 25/Jul/17

$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\:.\:\mathrm{tan}\:{x}}{{x}\:\mathrm{sin}\:{x}\:+\:\mathrm{2sin}^{\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{2}}{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\:.\:\mathrm{tan}\:{x}}{\mathrm{sin}\:{x}\:\left({x}\:+\:\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}\right)} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{\mathrm{sin}\:{x}}\:.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:{x}}{{x}\:+\:\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}} \\ $$$$\Rightarrow\:\mathrm{1}\:.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{tan}\:{x}}{{x}}}{\frac{{x}\:+\:\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}}{{x}}}\:=\:\mathrm{1}\:.\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{Is}\:\mathrm{this}\:\mathrm{correct}? \\ $$
Commented by mrW1 last updated on 26/Jul/17
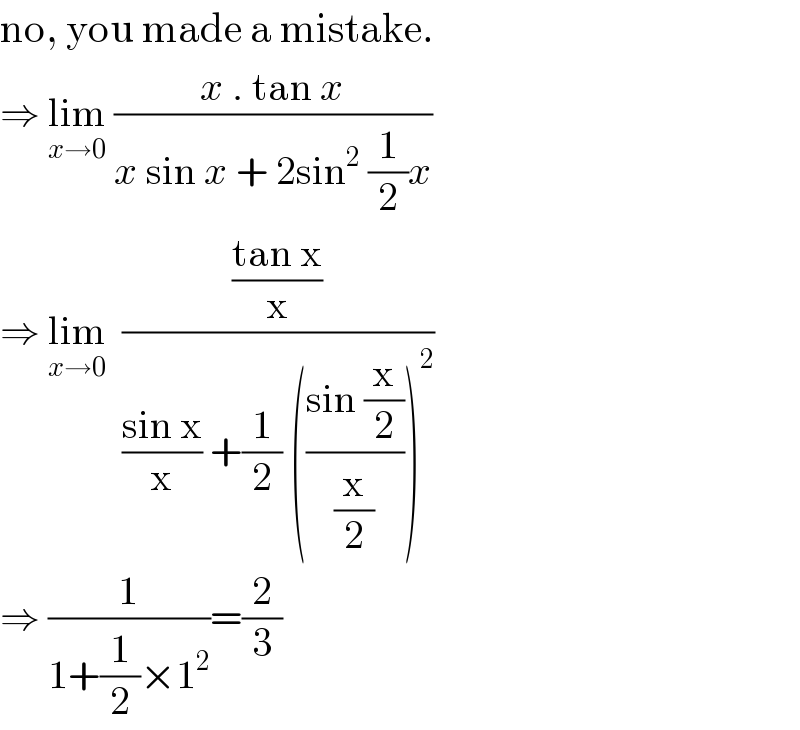
$$\mathrm{no},\:\mathrm{you}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake}. \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\:.\:\mathrm{tan}\:{x}}{{x}\:\mathrm{sin}\:{x}\:+\:\mathrm{2sin}^{\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{2}}{x}}\: \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{x}}}{\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\left(\frac{\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}}{\frac{\mathrm{x}}{\mathrm{2}}}\right)^{\mathrm{2}} }\: \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
