Question Number 131033 by greg_ed last updated on 31/Jan/21
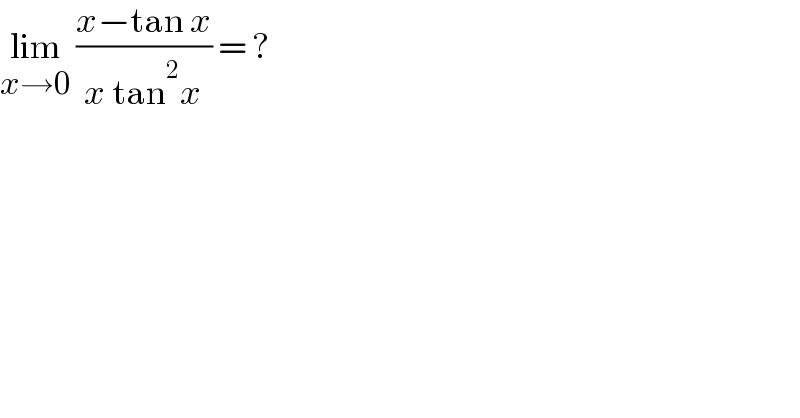
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}−\mathrm{tan}\:{x}}{{x}\:\mathrm{tan}^{\mathrm{2}} {x}}\:=\:? \\ $$
Commented by greg_ed last updated on 02/Feb/21

$$\boldsymbol{\mathrm{without}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{limited}}\:\boldsymbol{\mathrm{development}}\:\boldsymbol{\mathrm{method}}\:! \\ $$
Answered by Dwaipayan Shikari last updated on 31/Jan/21
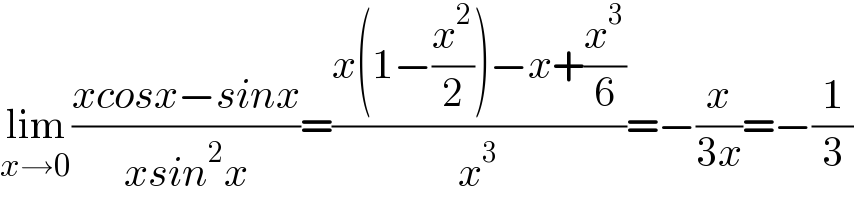
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{xcosx}−{sinx}}{{xsin}^{\mathrm{2}} {x}}=\frac{{x}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{{x}^{\mathrm{3}} }=−\frac{{x}}{\mathrm{3}{x}}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by mathmax by abdo last updated on 31/Jan/21
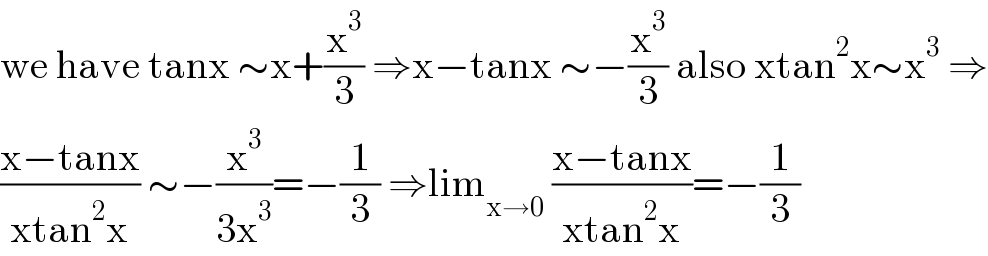
$$\mathrm{we}\:\mathrm{have}\:\mathrm{tanx}\:\sim\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\:\Rightarrow\mathrm{x}−\mathrm{tanx}\:\sim−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\:\mathrm{also}\:\mathrm{xtan}^{\mathrm{2}} \mathrm{x}\sim\mathrm{x}^{\mathrm{3}} \:\Rightarrow \\ $$$$\frac{\mathrm{x}−\mathrm{tanx}}{\mathrm{xtan}^{\mathrm{2}} \mathrm{x}}\:\sim−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3x}^{\mathrm{3}} }=−\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{x}−\mathrm{tanx}}{\mathrm{xtan}^{\mathrm{2}} \mathrm{x}}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
