Question Number 85061 by M±th+et£s last updated on 18/Mar/20
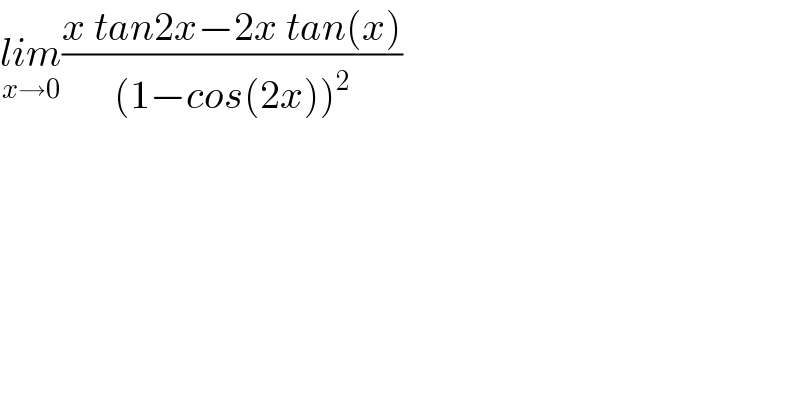
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{x}\:{tan}\mathrm{2}{x}−\mathrm{2}{x}\:{tan}\left({x}\right)}{\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 18/Mar/20
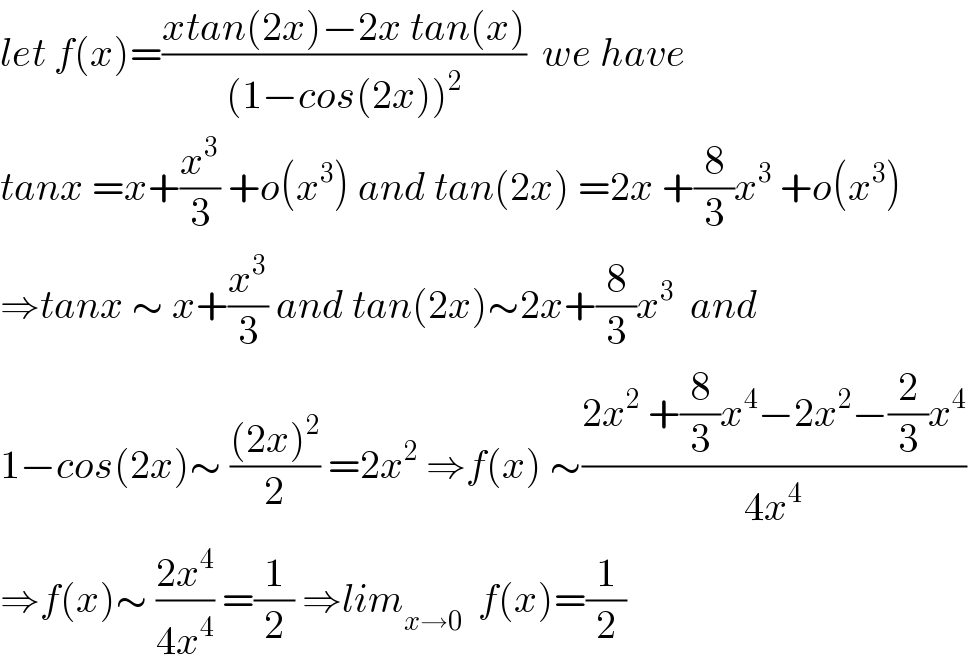
$${let}\:{f}\left({x}\right)=\frac{{xtan}\left(\mathrm{2}{x}\right)−\mathrm{2}{x}\:{tan}\left({x}\right)}{\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} }\:\:{we}\:{have}\: \\ $$$${tanx}\:={x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+{o}\left({x}^{\mathrm{3}} \right)\:{and}\:{tan}\left(\mathrm{2}{x}\right)\:=\mathrm{2}{x}\:+\frac{\mathrm{8}}{\mathrm{3}}{x}^{\mathrm{3}} \:+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\Rightarrow{tanx}\:\sim\:{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:{and}\:{tan}\left(\mathrm{2}{x}\right)\sim\mathrm{2}{x}+\frac{\mathrm{8}}{\mathrm{3}}{x}^{\mathrm{3}} \:\:{and} \\ $$$$\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\sim\:\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}\:=\mathrm{2}{x}^{\mathrm{2}} \:\Rightarrow{f}\left({x}\right)\:\sim\frac{\mathrm{2}{x}^{\mathrm{2}} \:+\frac{\mathrm{8}}{\mathrm{3}}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{4}} }{\mathrm{4}{x}^{\mathrm{4}} }\: \\ $$$$\Rightarrow{f}\left({x}\right)\sim\:\frac{\mathrm{2}{x}^{\mathrm{4}} }{\mathrm{4}{x}^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by M±th+et£s last updated on 18/Mar/20

$${thanks} \\ $$
Commented by mathmax by abdo last updated on 18/Mar/20

$${you}\:{are}\:{welcome} \\ $$
Answered by john santu last updated on 19/Mar/20
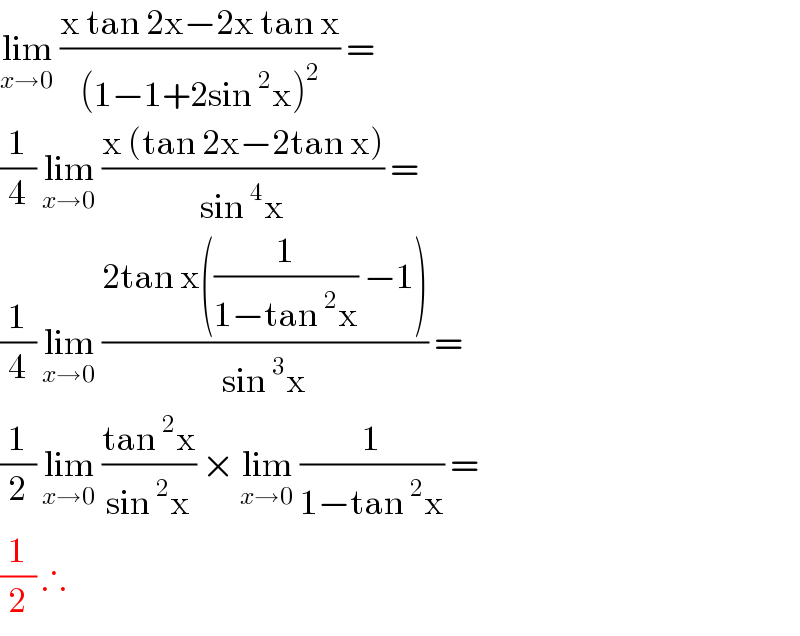
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}\:\mathrm{tan}\:\mathrm{2x}−\mathrm{2x}\:\mathrm{tan}\:\mathrm{x}}{\left(\mathrm{1}−\mathrm{1}+\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }\:=\: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}\:\left(\mathrm{tan}\:\mathrm{2x}−\mathrm{2tan}\:\mathrm{x}\right)}{\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}}\:=\: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2tan}\:\mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:−\mathrm{1}\right)}{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}\:=\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\therefore \\ $$
Commented by M±th+et£s last updated on 19/Mar/20

$${thank}\:{you}\:{sir} \\ $$
