Question Number 25588 by behi.8.3.4.17@gmail.com last updated on 11/Dec/17
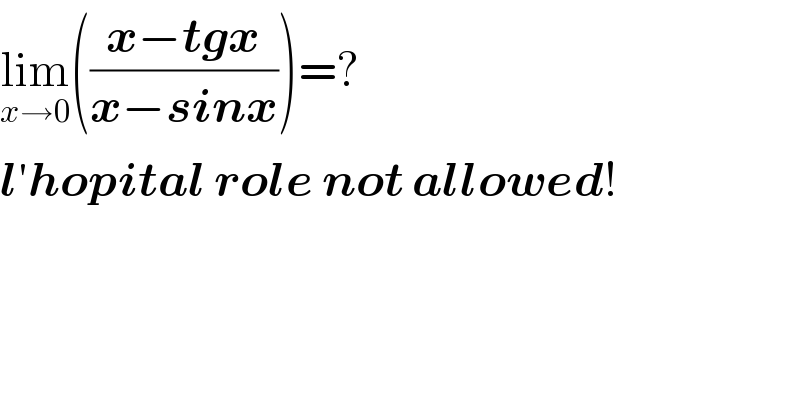
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\boldsymbol{{x}}−\boldsymbol{{tgx}}}{\boldsymbol{{x}}−\boldsymbol{{sinx}}}\right)=? \\ $$$$\boldsymbol{{l}}'\boldsymbol{{hopital}}\:\boldsymbol{{role}}\:\boldsymbol{{not}}\:\boldsymbol{{allowed}}! \\ $$
Commented by moxhix last updated on 12/Dec/17
https://math.stackexchange.com/questions/508733/lim-x-to0-fracx-sin-xx-tan-x-without-using-lhopital
.
Answered by kaivan.ahmadi last updated on 13/Dec/17
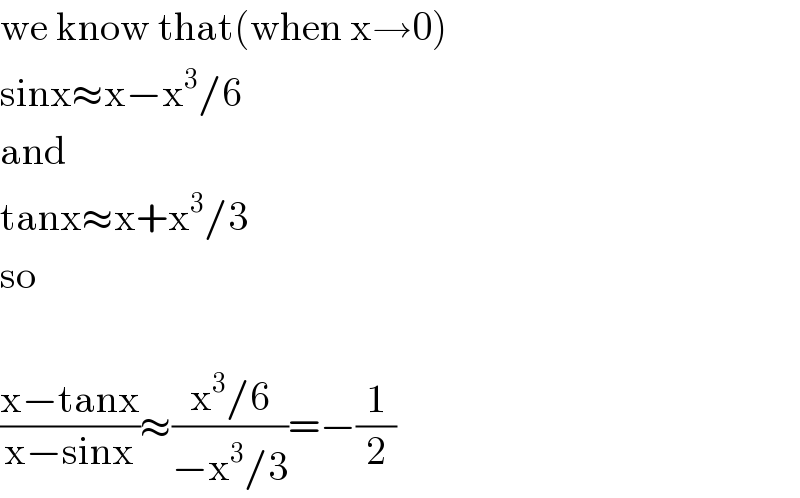
$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\left(\mathrm{when}\:\mathrm{x}\rightarrow\mathrm{0}\right) \\ $$$$\mathrm{sinx}\approx\mathrm{x}−\mathrm{x}^{\mathrm{3}} /\mathrm{6} \\ $$$$\mathrm{and} \\ $$$$\mathrm{tanx}\approx\mathrm{x}+\mathrm{x}^{\mathrm{3}} /\mathrm{3} \\ $$$$\mathrm{so} \\ $$$$ \\ $$$$\frac{\mathrm{x}−\mathrm{tanx}}{\mathrm{x}−\mathrm{sinx}}\approx\frac{\mathrm{x}^{\mathrm{3}} /\mathrm{6}}{−\mathrm{x}^{\mathrm{3}} /\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
