Question Number 121031 by bramlexs22 last updated on 05/Nov/20
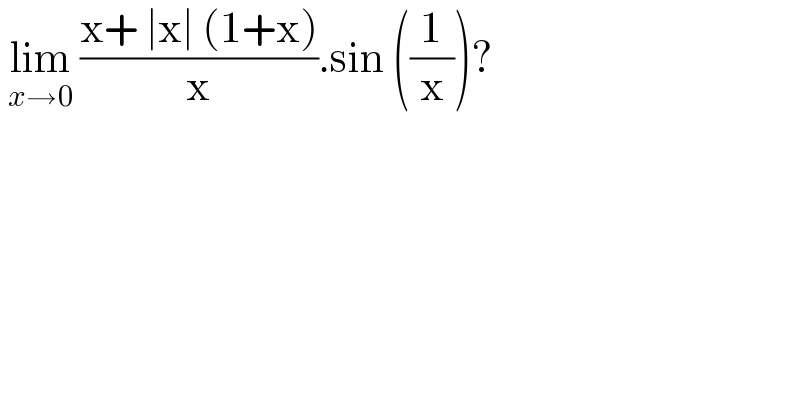
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}+\:\mid\mathrm{x}\mid\:\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)? \\ $$
Commented by liberty last updated on 05/Nov/20

$$\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{\mathrm{x}+\mid\mathrm{x}\mid\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{\mathrm{x}−\mathrm{x}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:=\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:−\mathrm{x}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{0} \\ $$$$\mathrm{but}\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{x}+\mid\mathrm{x}\mid\:\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{2x}+\mathrm{x}^{\mathrm{2}} }{\mathrm{x}}.\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{2}+\mathrm{x}\right).\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\mathrm{which}\:\mathrm{takes}\:\mathrm{on}\:\mathrm{every}\:\mathrm{value}\:\mathrm{between}\:−\mathrm{2}\:\mathrm{and}\:\mathrm{2} \\ $$$$\mathrm{in}\:\mathrm{every}\:\mathrm{interval}\:\left(\mathrm{0},\delta\right).\:\mathrm{Hence}\:\mathrm{g}\left(\mathrm{x}\right)=\left(\mathrm{2}+\mathrm{x}\right).\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\mathrm{does}\:\mathrm{not}\:\mathrm{approach}\:\mathrm{a}\:\mathrm{right}−\mathrm{hand}\:\mathrm{limit} \\ $$$$\mathrm{at}\:\mathrm{x}\rightarrow\mathrm{0}\:\mathrm{from}\:\mathrm{the}\:\mathrm{right}.\:\mathrm{This}\:\mathrm{shows} \\ $$$$\mathrm{that}\:\mathrm{a}\:\mathrm{function}\:\mathrm{may}\:\mathrm{have}\:\mathrm{a}\:\mathrm{limit}\:\mathrm{from} \\ $$$$\mathrm{one}\:\mathrm{side}\:\mathrm{at}\:\mathrm{a}\:\mathrm{point}\:\mathrm{but}\:\mathrm{fail}\:\mathrm{to}\:\mathrm{have}\:\mathrm{a}\:\mathrm{limit} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{other}\:\mathrm{side}.\:\blacktriangle \\ $$
