Question Number 149830 by DonQuichote last updated on 07/Aug/21
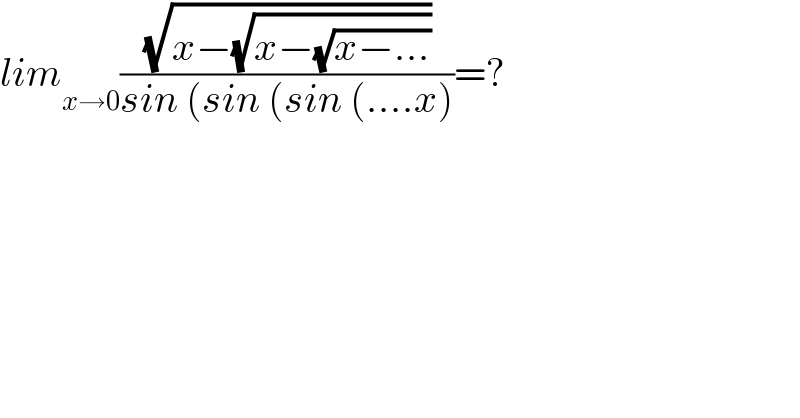
$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\sqrt{{x}−\sqrt{{x}−\sqrt{{x}−…}}}}{{sin}\:\left({sin}\:\left({sin}\:\left(….{x}\right)\right.\right.}=? \\ $$
Answered by mathmax by abdo last updated on 08/Aug/21
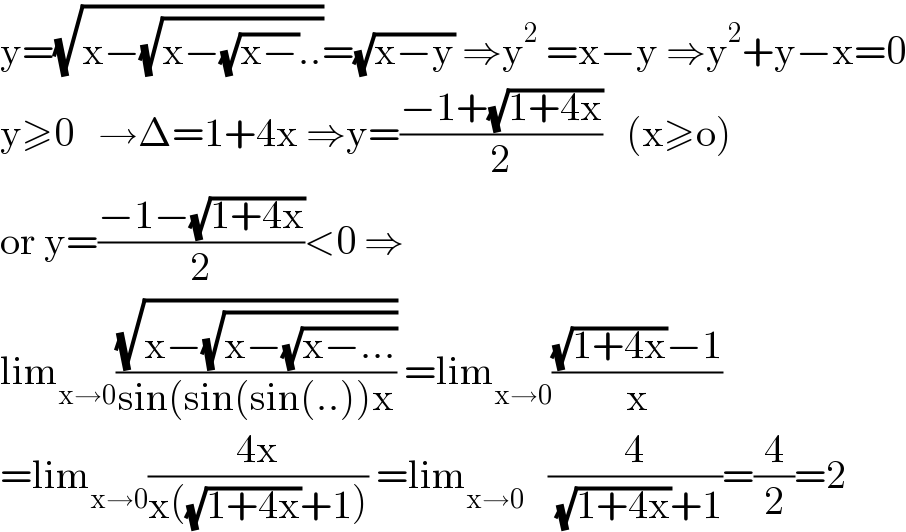
$$\mathrm{y}=\sqrt{\mathrm{x}−\sqrt{\mathrm{x}−\sqrt{\mathrm{x}−}..}}=\sqrt{\mathrm{x}−\mathrm{y}}\:\Rightarrow\mathrm{y}^{\mathrm{2}} \:=\mathrm{x}−\mathrm{y}\:\Rightarrow\mathrm{y}^{\mathrm{2}} +\mathrm{y}−\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{y}\geqslant\mathrm{0}\:\:\:\rightarrow\Delta=\mathrm{1}+\mathrm{4x}\:\Rightarrow\mathrm{y}=\frac{−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4x}}}{\mathrm{2}}\:\:\:\left(\mathrm{x}\geqslant\mathrm{o}\right) \\ $$$$\mathrm{or}\:\mathrm{y}=\frac{−\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{4x}}}{\mathrm{2}}<\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\sqrt{\mathrm{x}−\sqrt{\mathrm{x}−\sqrt{\mathrm{x}−…}}}}{\mathrm{sin}\left(\mathrm{sin}\left(\mathrm{sin}\left(..\right)\right)\mathrm{x}\right.}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\sqrt{\mathrm{1}+\mathrm{4x}}−\mathrm{1}}{\mathrm{x}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\mathrm{4x}}{\mathrm{x}\left(\sqrt{\mathrm{1}+\mathrm{4x}}+\mathrm{1}\right)}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{1}+\mathrm{4x}}+\mathrm{1}}=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$
