Question Number 174841 by infinityaction last updated on 12/Aug/22
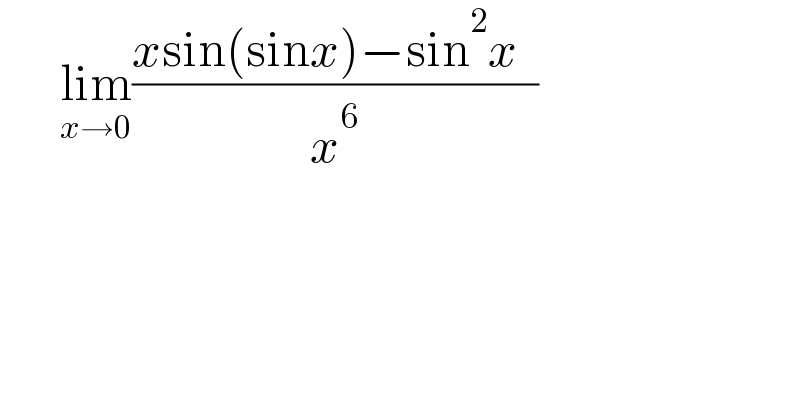
$$\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\mathrm{sin}\left(\mathrm{sin}{x}\right)−\mathrm{sin}^{\mathrm{2}} {x}\:\:}{{x}^{\mathrm{6}} } \\ $$
Answered by Ar Brandon last updated on 12/Aug/22

$$\mathcal{A}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\mathrm{sin}\left(\mathrm{sin}{x}\right)−\mathrm{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{6}} } \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\left(\mathrm{sin}{x}−\frac{\mathrm{sin}^{\mathrm{3}} {x}}{\mathrm{6}}\right)−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)^{\mathrm{2}} }{{x}^{\mathrm{6}} } \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{6}}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)^{\mathrm{3}} \right)−\left({x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{3}}+\frac{{x}^{\mathrm{6}} }{\mathrm{36}}\right)}{{x}^{\mathrm{6}} } \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{6}} }\left\{{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{4}} }{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{6}}\left({x}^{\mathrm{4}} −\frac{{x}^{\mathrm{6}} }{\mathrm{2}}+\frac{{x}^{\mathrm{8}} }{\mathrm{12}}−\frac{{x}^{\mathrm{10}} }{\mathrm{216}}\right)−{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{3}}−\frac{{x}^{\mathrm{6}} }{\mathrm{36}}\right\} \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{6}} }\left(\frac{{x}^{\mathrm{6}} }{\mathrm{18}}−\frac{{x}^{\mathrm{8}} }{\mathrm{72}}+\frac{{x}^{\mathrm{10}} }{\mathrm{1296}}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{18}}−\frac{{x}^{\mathrm{2}} }{\mathrm{72}}+\frac{{x}^{\mathrm{4}} }{\mathrm{1296}}\right)=\frac{\mathrm{1}}{\mathrm{18}} \\ $$
Commented by infinityaction last updated on 12/Aug/22

$${thank}\:{you}\:{sir} \\ $$
