Question Number 115318 by bemath last updated on 25/Sep/20
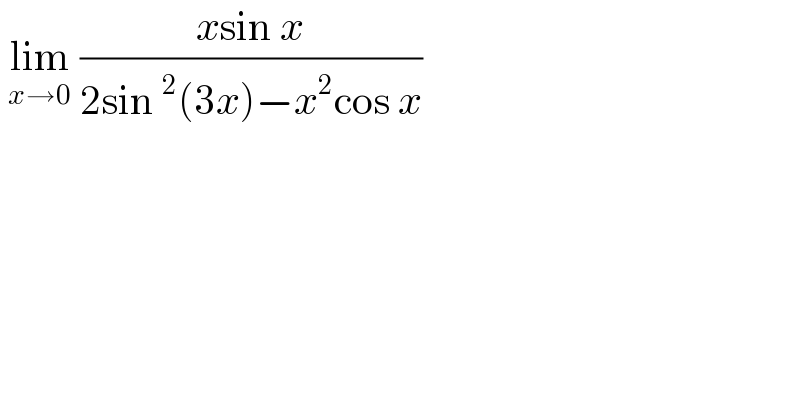
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\mathrm{sin}\:{x}}{\mathrm{2sin}\:^{\mathrm{2}} \left(\mathrm{3}{x}\right)−{x}^{\mathrm{2}} \mathrm{cos}\:{x}} \\ $$
Answered by bobhans last updated on 25/Sep/20
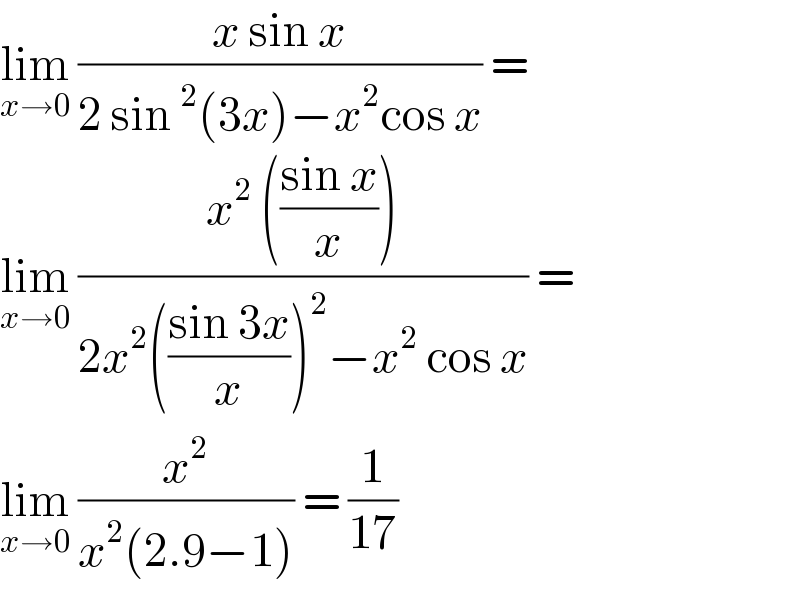
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\:\mathrm{sin}\:{x}}{\mathrm{2}\:\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{3}{x}\right)−{x}^{\mathrm{2}} \mathrm{cos}\:{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \:\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)}{\mathrm{2}{x}^{\mathrm{2}} \left(\frac{\mathrm{sin}\:\mathrm{3}{x}}{{x}}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} \:\mathrm{cos}\:{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left(\mathrm{2}.\mathrm{9}−\mathrm{1}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{17}} \\ $$
Answered by Bird last updated on 25/Sep/20
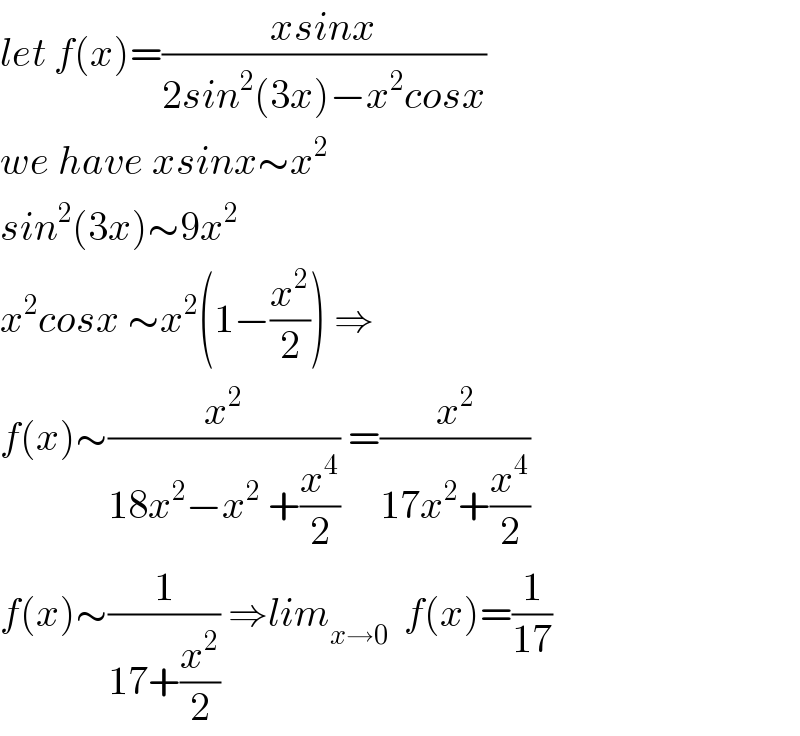
$${let}\:{f}\left({x}\right)=\frac{{xsinx}}{\mathrm{2}{sin}^{\mathrm{2}} \left(\mathrm{3}{x}\right)−{x}^{\mathrm{2}} {cosx}} \\ $$$${we}\:{have}\:{xsinx}\sim{x}^{\mathrm{2}} \\ $$$${sin}^{\mathrm{2}} \left(\mathrm{3}{x}\right)\sim\mathrm{9}{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {cosx}\:\sim{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{{x}^{\mathrm{2}} }{\mathrm{18}{x}^{\mathrm{2}} −{x}^{\mathrm{2}} \:+\frac{{x}^{\mathrm{4}} }{\mathrm{2}}}\:=\frac{{x}^{\mathrm{2}} }{\mathrm{17}{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{2}}} \\ $$$${f}\left({x}\right)\sim\frac{\mathrm{1}}{\mathrm{17}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{17}} \\ $$
