Question Number 101239 by M±th+et+s last updated on 01/Jul/20
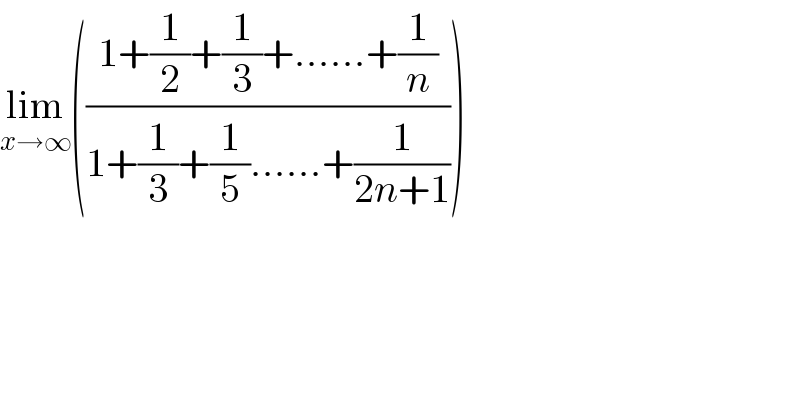
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+……+\frac{\mathrm{1}}{{n}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}……+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}}\right) \\ $$
Answered by mathmax by abdo last updated on 01/Jul/20
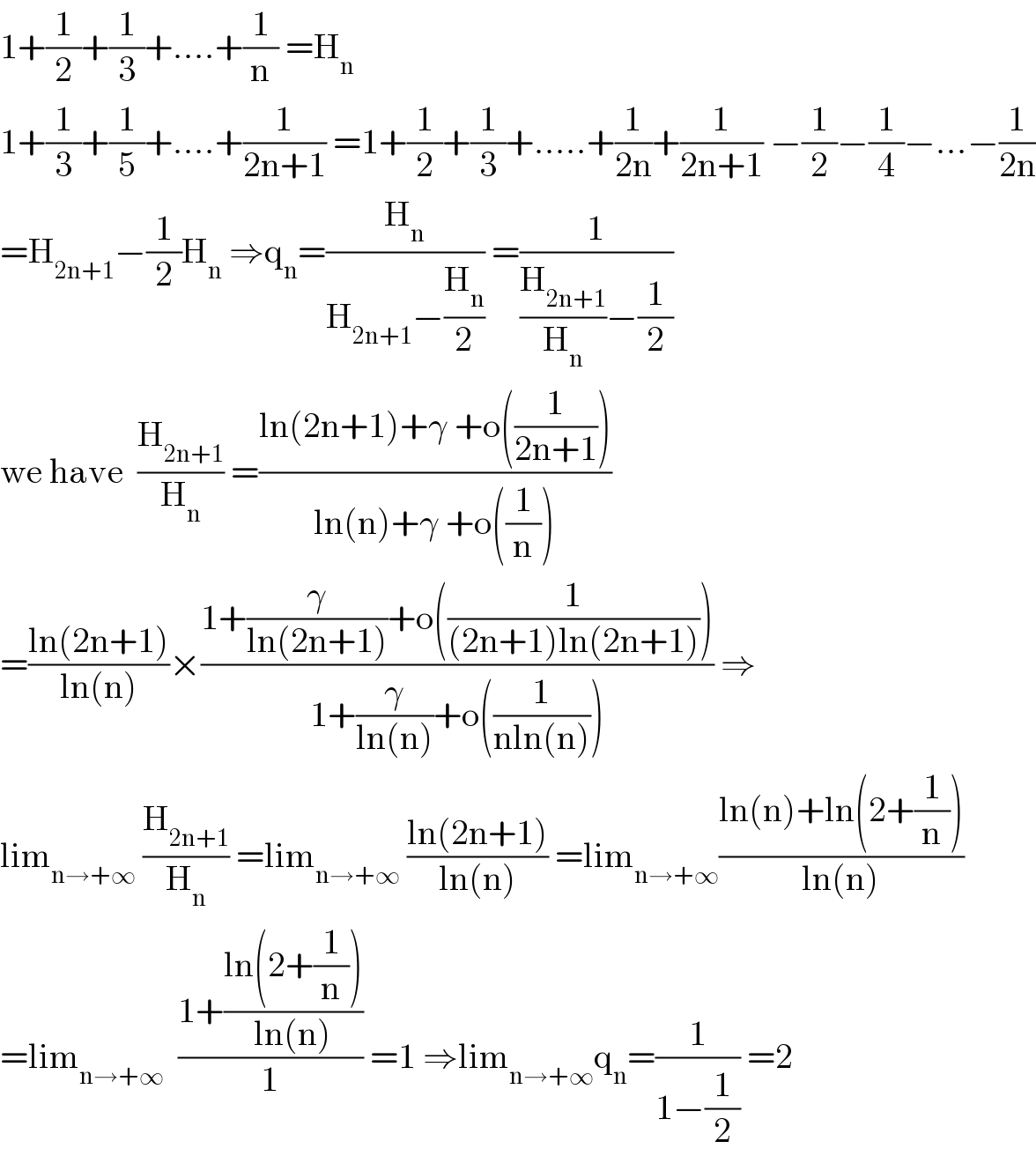
$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+….+\frac{\mathrm{1}}{\mathrm{n}}\:=\mathrm{H}_{\mathrm{n}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+….+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…..+\frac{\mathrm{1}}{\mathrm{2n}}+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}−…−\frac{\mathrm{1}}{\mathrm{2n}} \\ $$$$=\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} \:\Rightarrow\mathrm{q}_{\mathrm{n}} =\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{2}}}\:=\frac{\mathrm{1}}{\frac{\mathrm{H}_{\mathrm{2n}+\mathrm{1}} }{\mathrm{H}_{\mathrm{n}} }−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\:\frac{\mathrm{H}_{\mathrm{2n}+\mathrm{1}} }{\mathrm{H}_{\mathrm{n}} }\:=\frac{\mathrm{ln}\left(\mathrm{2n}+\mathrm{1}\right)+\gamma\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\right)}{\mathrm{ln}\left(\mathrm{n}\right)+\gamma\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)} \\ $$$$=\frac{\mathrm{ln}\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{ln}\left(\mathrm{n}\right)}×\frac{\mathrm{1}+\frac{\gamma}{\mathrm{ln}\left(\mathrm{2n}+\mathrm{1}\right)}+\mathrm{o}\left(\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{ln}\left(\mathrm{2n}+\mathrm{1}\right)}\right)}{\mathrm{1}+\frac{\gamma}{\mathrm{ln}\left(\mathrm{n}\right)}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{nln}\left(\mathrm{n}\right)}\right)}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{H}_{\mathrm{2n}+\mathrm{1}} }{\mathrm{H}_{\mathrm{n}} }\:=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{ln}\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{ln}\left(\mathrm{n}\right)}\:=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{ln}\left(\mathrm{n}\right)+\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{ln}\left(\mathrm{n}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\frac{\mathrm{1}+\frac{\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{ln}\left(\mathrm{n}\right)}}{\mathrm{1}}\:=\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{q}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\:=\mathrm{2} \\ $$
Commented by M±th+et+s last updated on 01/Jul/20

$${well}\:{done} \\ $$
Commented by mathmax by abdo last updated on 01/Jul/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
