Menu Close

lim-x-1-1-2n-n-e-1-2-n-n-e-2-

Tinku Tara 0 Comments
Pin




Question Number 119867 by Study last updated on 27/Oct/20
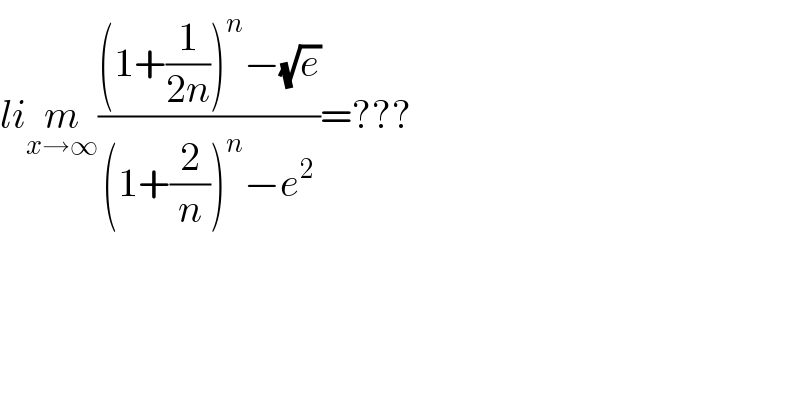
lim_(x→∞) (((1+(1/(2n)))^n −(√e))/((1+(2/n))^n −e^2 ))=???
$${li}\underset{{x}\rightarrow\infty} {{m}}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)^{{n}} −\sqrt{{e}}}{\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)^{{n}} −{e}^{\mathrm{2}} }=??? \\ $$
Commented by Dwaipayan Shikari last updated on 27/Oct/20
(1/(16))e^(−(3/2))
$$\frac{\mathrm{1}}{\mathrm{16}}{e}^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$
Commented by Ar Brandon last updated on 27/Oct/20
lim_(x→∞) (((1+(1/(2n)))^n −(√e))/((1+(2/n))^n −e^2 ))=lim_(x→∞) (((1+(1/(2n)))^(2n∙(1/2)) −(√e))/((1+(2/n))^((n/2)∙2) −e^2 )) =(((√e)−(√e))/(e^2 −e^2 )) {since lim_(x→∞) (1+(1/x))^x =e} =(((√e)−(√e))/(((√e)−(√e))((√e)+(√e))(e+e)))=(1/(2(√e)×2e))=(1/4)e^(−3/2) Greetings to mr Rasheed. It′s been quite a long time. Hope you′re doing well Sir!
$$\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}}\right)^{\mathrm{n}} −\sqrt{\mathrm{e}}}{\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{n}}\right)^{\mathrm{n}} −\mathrm{e}^{\mathrm{2}} }=\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2n}}\right)^{\mathrm{2n}\centerdot\frac{\mathrm{1}}{\mathrm{2}}} −\sqrt{\mathrm{e}}}{\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{n}}\right)^{\frac{\mathrm{n}}{\mathrm{2}}\centerdot\mathrm{2}} −\mathrm{e}^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{\mathrm{e}}−\sqrt{\mathrm{e}}}{\mathrm{e}^{\mathrm{2}} −\mathrm{e}^{\mathrm{2}} }\:\:\:\:\left\{\mathrm{since}\:\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{x}} =\mathrm{e}\right\} \\ $$$$=\frac{\sqrt{\mathrm{e}}−\sqrt{\mathrm{e}}}{\left(\sqrt{\mathrm{e}}−\sqrt{\mathrm{e}}\right)\left(\sqrt{\mathrm{e}}+\sqrt{\mathrm{e}}\right)\left(\mathrm{e}+\mathrm{e}\right)}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{e}}×\mathrm{2e}}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{3}/\mathrm{2}} \\ $$$$ \\ $$$${Greetings}\:{to}\:{mr}\:{Rasheed}.\:{It}'{s}\:{been}\:{quite} \\ $$$${a}\:{long}\:{time}.\:{Hope}\:{you}'{re}\:{doing}\:{well}\:{Sir}! \\ $$
Answered by TANMAY PANACEA last updated on 27/Oct/20
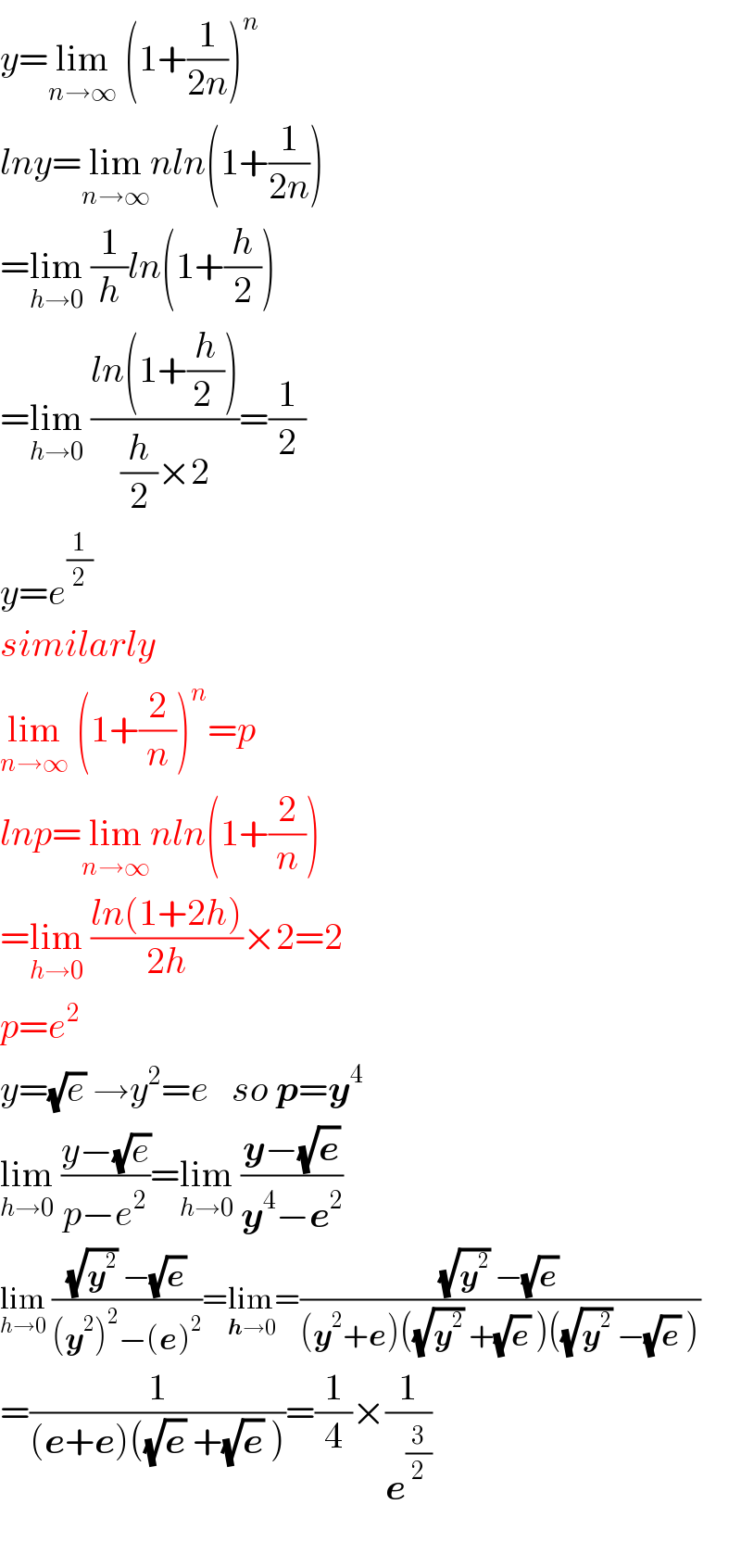
y=lim_(n→∞) (1+(1/(2n)))^n lny=lim_(n→∞) nln(1+(1/(2n))) =lim_(h→0) (1/h)ln(1+(h/2)) =lim_(h→0) ((ln(1+(h/(2 ))))/((h/2)×2))=(1/2) y=e^(1/2) similarly lim_(n→∞) (1+(2/n))^n =p lnp=lim_(n→∞) nln(1+(2/n)) =lim_(h→0) ((ln(1+2h))/(2h))×2=2 p=e^2 y=(√e) →y^2 =e so p=y^4 lim_(h→0) ((y−(√e))/(p−e^2 ))=lim_(h→0) ((y−(√e))/(y^4 −e^2 )) lim_(h→0) (((√y^2 ) −(√e))/((y^2 )^2 −(e)^2 ))=lim_(h→0) =(((√y^2 ) −(√e))/((y^2 +e)((√y^2 ) +(√e) )((√y^2 ) −(√e) ))) =(1/((e+e)((√e) +(√e) )))=(1/4)×(1/e^(3/2) )
$${y}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)^{{n}} \\ $$$${lny}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{h}}{ln}\left(\mathrm{1}+\frac{{h}}{\mathrm{2}}\right) \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}+\frac{{h}}{\mathrm{2}\:}\right)}{\frac{{h}}{\mathrm{2}}×\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}={e}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${similarly}\: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)^{{n}} ={p} \\ $$$${lnp}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{nln}\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right) \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}+\mathrm{2}{h}\right)}{\mathrm{2}{h}}×\mathrm{2}=\mathrm{2} \\ $$$${p}={e}^{\mathrm{2}} \\ $$$${y}=\sqrt{{e}}\:\rightarrow{y}^{\mathrm{2}} ={e}\:\:\:{so}\:\boldsymbol{{p}}=\boldsymbol{{y}}^{\mathrm{4}} \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{y}−\sqrt{{e}}}{{p}−{e}^{\mathrm{2}} }=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{y}}−\sqrt{\boldsymbol{{e}}}}{\boldsymbol{{y}}^{\mathrm{4}} −\boldsymbol{{e}}^{\mathrm{2}} } \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\boldsymbol{{y}}^{\mathrm{2}} }\:−\sqrt{\boldsymbol{{e}}}}{\left(\boldsymbol{{y}}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\boldsymbol{{e}}\right)^{\mathrm{2}} }=\underset{\boldsymbol{{h}}\rightarrow\mathrm{0}} {\mathrm{lim}}=\frac{\sqrt{\boldsymbol{{y}}^{\mathrm{2}} }\:−\sqrt{\boldsymbol{{e}}}}{\left(\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{e}}\right)\left(\sqrt{\boldsymbol{{y}}^{\mathrm{2}} }\:+\sqrt{\boldsymbol{{e}}}\:\right)\left(\sqrt{\boldsymbol{{y}}^{\mathrm{2}} }\:−\sqrt{\boldsymbol{{e}}}\:\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\boldsymbol{{e}}+\boldsymbol{{e}}\right)\left(\sqrt{\boldsymbol{{e}}}\:+\sqrt{\boldsymbol{{e}}}\:\right)}=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\boldsymbol{{e}}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *