Question Number 127459 by liberty last updated on 30/Dec/20
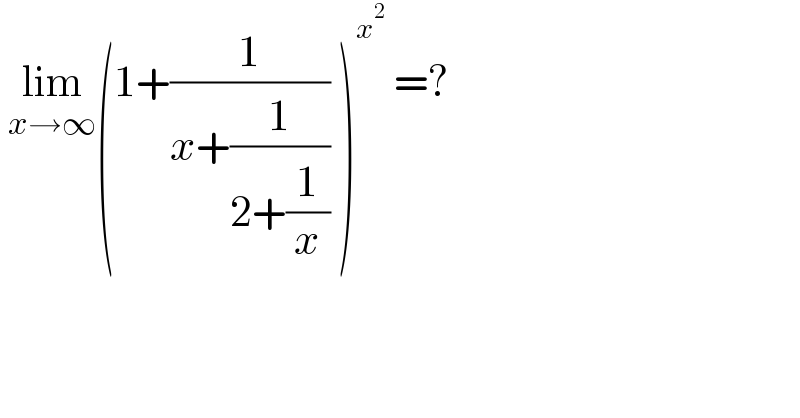
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{{x}}}}\:\right)^{{x}^{\mathrm{2}} } \:=?\: \\ $$
Answered by john_santu last updated on 30/Dec/20

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{x}}}}\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}+\frac{\mathrm{x}}{\mathrm{2x}+\mathrm{1}}}\:=\:\mathrm{1}+\frac{\mathrm{1}}{\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}}{\mathrm{2x}+\mathrm{1}}} \\ $$$$\:\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}}{\mathrm{2x}+\mathrm{1}}}\right)^{\mathrm{x}^{\mathrm{2}} } \:=\: \\ $$$$\:\:\:\:\:\:\mathrm{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}}{\mathrm{2x}+\mathrm{1}}}\:−\mathrm{1}\:\right).\:\mathrm{x}^{\mathrm{2}} } = \\ $$$$\:\:\:\:\:\:\mathrm{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}}\right).\mathrm{x}^{\mathrm{2}} } =\:\mathrm{e}^{\infty} \:=\:\infty\: \\ $$$$ \\ $$
