Question Number 148654 by mathdanisur last updated on 29/Jul/21
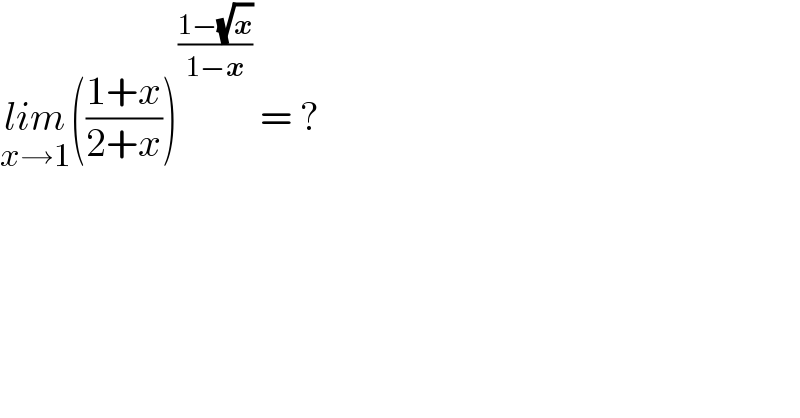
$$\underset{{x}\rightarrow\mathrm{1}} {{lim}}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\mathrm{1}−\sqrt{\boldsymbol{{x}}}}{\mathrm{1}−\boldsymbol{{x}}}} \:=\:? \\ $$
Answered by ArielVyny last updated on 29/Jul/21
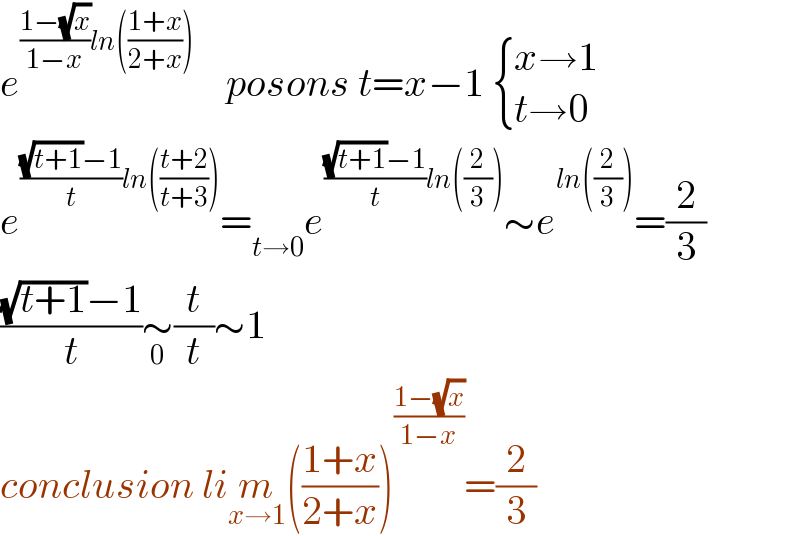
$${e}^{\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}−{x}}{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)} \:\:\:\:{posons}\:{t}={x}−\mathrm{1}\:\begin{cases}{{x}\rightarrow\mathrm{1}}\\{{t}\rightarrow\mathrm{0}}\end{cases} \\ $$$${e}^{\frac{\sqrt{{t}+\mathrm{1}}−\mathrm{1}}{{t}}{ln}\left(\frac{{t}+\mathrm{2}}{{t}+\mathrm{3}}\right)} =_{{t}\rightarrow\mathrm{0}} {e}^{\frac{\sqrt{{t}+\mathrm{1}}−\mathrm{1}}{{t}}{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)} \sim{e}^{{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\frac{\sqrt{{t}+\mathrm{1}}−\mathrm{1}}{{t}}\underset{\mathrm{0}} {\sim}\frac{{t}}{{t}}\sim\mathrm{1} \\ $$$${conclusion}\:{li}\underset{{x}\rightarrow\mathrm{1}} {{m}}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}−{x}}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 29/Jul/21
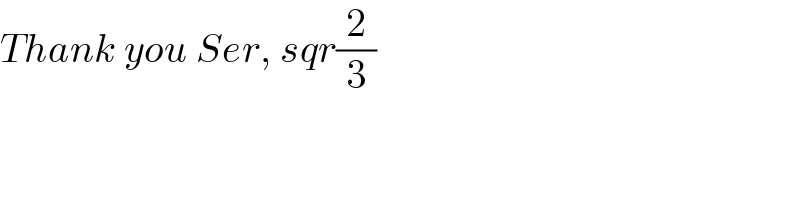
$${Thank}\:{you}\:{Ser},\:{sqr}\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by ArielVyny last updated on 29/Jul/21
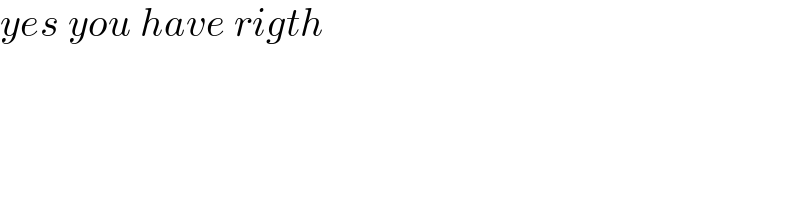
$${yes}\:{you}\:{have}\:{rigth} \\ $$
Answered by Rasheed.Sindhi last updated on 29/Jul/21

$$\underset{{x}\rightarrow\mathrm{1}} {{lim}}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\mathrm{1}−\sqrt{\boldsymbol{{x}}}}{\mathrm{1}−\boldsymbol{{x}}}} \: \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {{lim}}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\mathrm{1}−\sqrt{\boldsymbol{{x}}}}{\mathrm{1}−\left(\sqrt{{x}}\right)^{\mathrm{2}} }} \: \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {{lim}}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\cancel{\mathrm{1}−\sqrt{\boldsymbol{{x}}}}}{\left(\cancel{\mathrm{1}−\sqrt{{x}}\right)}\left(\mathrm{1}+\sqrt{{x}}\right)}} \: \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {{lim}}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\mathrm{1}}{\mathrm{1}+\sqrt{{x}}}} \:=\left(\frac{\mathrm{1}+\mathrm{1}}{\mathrm{2}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{1}}}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{1}/\mathrm{2}} \\ $$$$=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 29/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
Answered by liberty last updated on 30/Jul/21

$$\:\mathrm{T}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{2}+\mathrm{x}−\mathrm{1}}{\mathrm{2}+\mathrm{x}}\right)^{\frac{\mathrm{1}−\sqrt{\mathrm{x}}}{\left(\mathrm{1}+\sqrt{\mathrm{x}}\right)\left(\mathrm{1}−\sqrt{\mathrm{x}}\right)}} \\ $$$$\mathrm{T}=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}+\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{x}}}} \\ $$$$\:\mathrm{T}=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}=\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 30/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
Answered by mathmax by abdo last updated on 31/Jul/21
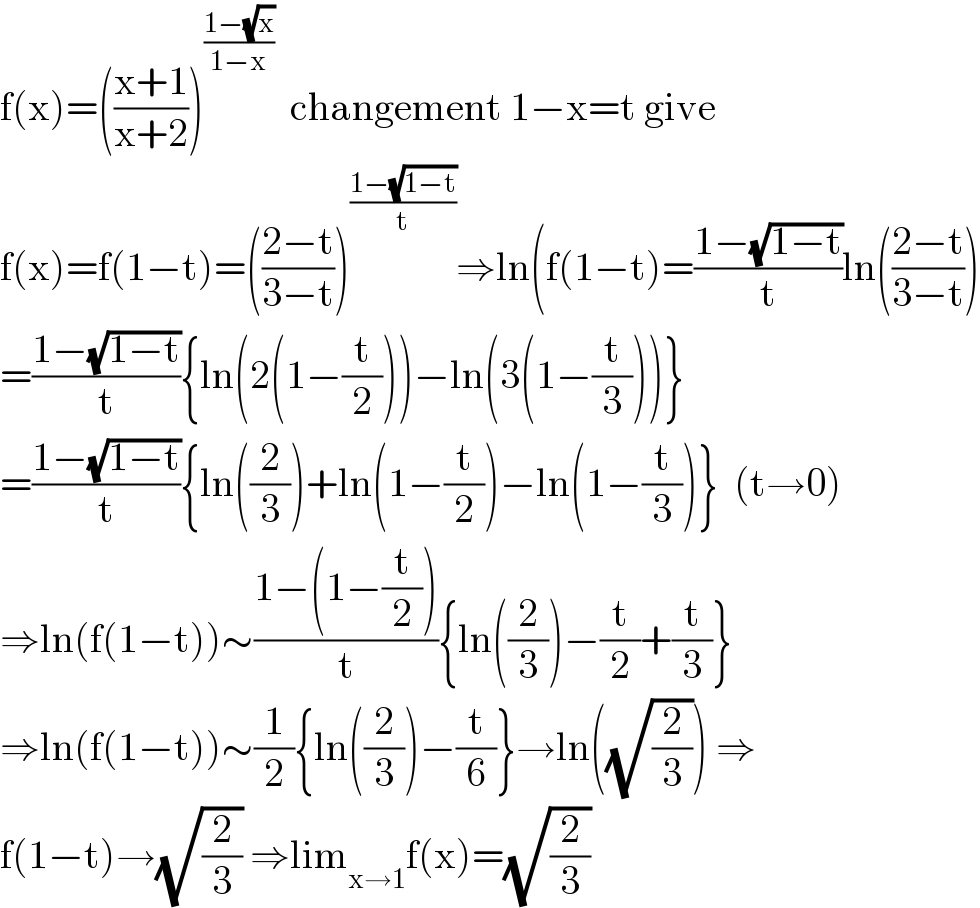
$$\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right)^{\frac{\mathrm{1}−\sqrt{\mathrm{x}}}{\mathrm{1}−\mathrm{x}}} \:\:\mathrm{changement}\:\mathrm{1}−\mathrm{x}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{1}−\mathrm{t}\right)=\left(\frac{\mathrm{2}−\mathrm{t}}{\mathrm{3}−\mathrm{t}}\right)^{\frac{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{t}}}{\mathrm{t}}} \Rightarrow\mathrm{ln}\left(\mathrm{f}\left(\mathrm{1}−\mathrm{t}\right)=\frac{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{t}}}{\mathrm{t}}\mathrm{ln}\left(\frac{\mathrm{2}−\mathrm{t}}{\mathrm{3}−\mathrm{t}}\right)\right. \\ $$$$=\frac{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{t}}}{\mathrm{t}}\left\{\mathrm{ln}\left(\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{2}}\right)\right)−\mathrm{ln}\left(\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{3}}\right)\right)\right\} \\ $$$$=\frac{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{t}}}{\mathrm{t}}\left\{\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{2}}\right)−\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{3}}\right)\right\}\:\:\left(\mathrm{t}\rightarrow\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{ln}\left(\mathrm{f}\left(\mathrm{1}−\mathrm{t}\right)\right)\sim\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{2}}\right)}{\mathrm{t}}\left\{\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\frac{\mathrm{t}}{\mathrm{2}}+\frac{\mathrm{t}}{\mathrm{3}}\right\} \\ $$$$\Rightarrow\mathrm{ln}\left(\mathrm{f}\left(\mathrm{1}−\mathrm{t}\right)\right)\sim\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\frac{\mathrm{t}}{\mathrm{6}}\right\}\rightarrow\mathrm{ln}\left(\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{1}−\mathrm{t}\right)\rightarrow\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$
Commented by mathdanisur last updated on 01/Aug/21

$${Thank}\:{You}\:{Ser} \\ $$
