Question Number 122721 by bemath last updated on 19/Nov/20
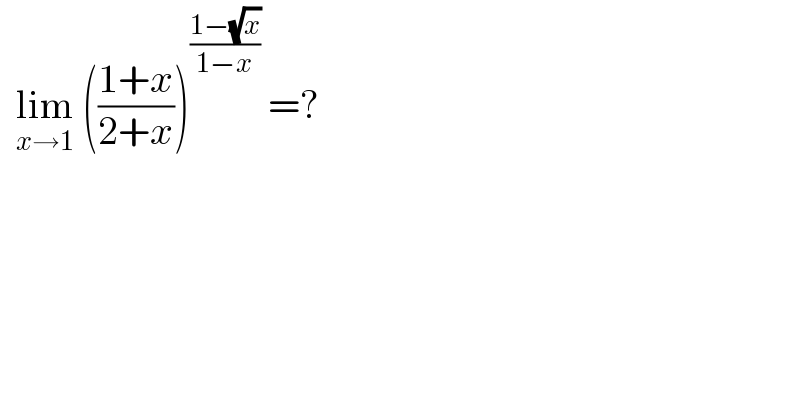
$$\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}−{x}}} \:=?\: \\ $$
Answered by Dwaipayan Shikari last updated on 19/Nov/20
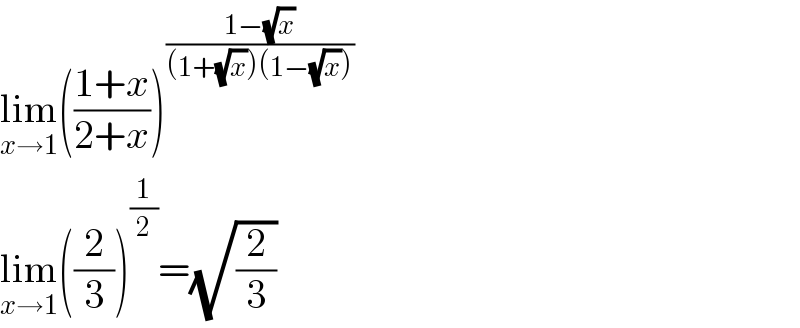
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\mathrm{1}−\sqrt{{x}}}{\left(\mathrm{1}+\sqrt{{x}}\right)\left(\mathrm{1}−\sqrt{{x}}\right)}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$
Answered by liberty last updated on 19/Nov/20
![Solve lim_(x→1) (((1+x)/(2+x)))^((1−(√x))/(1−x)) ? Solution : denote h(x)=((1+x)/(2+x)) ; r(x)=((1−(√x))/(1−x)) { ((lim_(x→1) h(x)= (2/3))),((lim_(x→1) r(x)=lim_(x→1) ((1−(√x))/((1+(√x))(1−(√x))))=(1/2))) :} but at finite limits lim_(x→a) h(x) = A>0 , lim_(x→a) r(x)= B the following relation holds true : lim_(x→a) (h(x))^(r(x)) = e^(lim_(x→a) r(x).ln h(x)) = e^(B.ln A) = A^B . Hence lim_(x→1) (((1+x)/(2+x)))^((1−(√x))/(1−x)) = ((2/3))^(1/2) =(√(2/3)) Note: If in handling examples of the form lim_(x→1) (h(x))^(r(x)) it turns out that lim_(x→a) h(x)=1 and lim_(x→a) r(x)=∞ , then the following transformation may be recomended : lim_(x→a) [ h(x)]^(r(x)) = lim_(x→a) {1+[ h(x)−1] }^(r(x)) = lim_(x→a) {[1+(h(x)−1)]^(1/(h(x)−1)) }^(r(x)[h(x)−1 ]) = e^(lim_(x→a) r(x) [h(x)−1 ] ) . ▲](https://www.tinkutara.com/question/Q122723.png)
$$\:{Solve}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}−{x}}} \:? \\ $$$$\:{Solution}\::\: \\ $$$$\:{denote}\:{h}\left({x}\right)=\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\:;\:{r}\left({x}\right)=\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}−{x}} \\ $$$$\:\begin{cases}{\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:{h}\left({x}\right)=\:\frac{\mathrm{2}}{\mathrm{3}}}\\{\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:{r}\left({x}\right)=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}−\sqrt{{x}}}{\left(\mathrm{1}+\sqrt{{x}}\right)\left(\mathrm{1}−\sqrt{{x}}\right)}=\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$$${but}\:{at}\:{finite}\:{limits}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{h}\left({x}\right)\:=\:{A}>\mathrm{0}\:, \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{r}\left({x}\right)=\:{B}\:{the}\:{following}\:{relation} \\ $$$${holds}\:{true}\::\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\left({h}\left({x}\right)\right)^{{r}\left({x}\right)} \:=\:{e}^{\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{r}\left({x}\right).\mathrm{ln}\:{h}\left({x}\right)} =\:{e}^{{B}.\mathrm{ln}\:{A}} \\ $$$$\:=\:{A}^{{B}} .\:{Hence}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}+{x}}{\mathrm{2}+{x}}\right)^{\frac{\mathrm{1}−\sqrt{{x}}}{\mathrm{1}−{x}}} =\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$${Note}:\:{If}\:{in}\:{handling}\:{examples}\:{of}\:{the} \\ $$$${form}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left({h}\left({x}\right)\right)^{{r}\left({x}\right)} \:{it}\:{turns}\:{out} \\ $$$${that}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{h}\left({x}\right)=\mathrm{1}\:{and}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{r}\left({x}\right)=\infty\:, \\ $$$${then}\:{the}\:{following}\:{transformation} \\ $$$${may}\:{be}\:{recomended}\::\: \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\left[\:{h}\left({x}\right)\right]^{{r}\left({x}\right)} \:=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\left\{\mathrm{1}+\left[\:{h}\left({x}\right)−\mathrm{1}\right]\:\right\}^{{r}\left({x}\right)} \\ $$$$=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\left\{\left[\mathrm{1}+\left({h}\left({x}\right)−\mathrm{1}\right)\right]^{\frac{\mathrm{1}}{{h}\left({x}\right)−\mathrm{1}}} \:\right\}^{{r}\left({x}\right)\left[{h}\left({x}\right)−\mathrm{1}\:\right]} \\ $$$$=\:{e}^{\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{r}\left({x}\right)\:\left[{h}\left({x}\right)−\mathrm{1}\:\right]\:} .\:\blacktriangle \\ $$$$ \\ $$
Commented by liberty last updated on 19/Nov/20
![for example find the limit : lim_(x→∞) (((2x^2 +8)/(2x^2 −5)))^(6x^2 +5) ? Solution : let us denote : h(x)=((2x^2 +8)/(2x^2 −5)) ; r(x)=6x^2 +5 lim_(x→∞) h(x)= lim_(x→∞) ((2x^2 +8)/(2x^2 −5)) = 1 lim_(x→∞) r(x)= lim_(x→∞) (6x^2 +5)=∞ use the formula lim_(x→∞) (((2x^2 +8)/(2x^2 −5)))^(6x^2 +5) = e^(lim_(x→∞) r(x) [h(x)−1 ]) ; [ h(x)−1=((13)/(2x^2 −5)) ] = e^(lim_(x→∞) (((13(6x^2 +5))/(2x^2 −5)))) = e^(39) . ✓▲](https://www.tinkutara.com/question/Q122724.png)
$${for}\:{example}\:{find}\:{the}\:{limit}\:: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}}\right)^{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{5}} ? \\ $$$${Solution}\::\:{let}\:{us}\:{denote}\::\: \\ $$$${h}\left({x}\right)=\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}}\:;\:{r}\left({x}\right)=\mathrm{6}{x}^{\mathrm{2}} +\mathrm{5}\: \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{h}\left({x}\right)=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}}\:=\:\mathrm{1}\: \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{r}\left({x}\right)=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{6}{x}^{\mathrm{2}} +\mathrm{5}\right)=\infty\: \\ $$$$\:{use}\:{the}\:{formula}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}}\right)^{\mathrm{6}{x}^{\mathrm{2}} +\mathrm{5}} \\ $$$$\:=\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}{r}\left({x}\right)\:\left[{h}\left({x}\right)−\mathrm{1}\:\right]} ;\:\left[\:{h}\left({x}\right)−\mathrm{1}=\frac{\mathrm{13}}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}}\:\right] \\ $$$$=\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{13}\left(\mathrm{6}{x}^{\mathrm{2}} +\mathrm{5}\right)}{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}}\right)} \:=\:{e}^{\mathrm{39}} .\:\checkmark\blacktriangle \\ $$
Commented by bemath last updated on 19/Nov/20
$${waww}…{gave}\:{kudos} \\ $$
