Question Number 92291 by jagoll last updated on 06/May/20
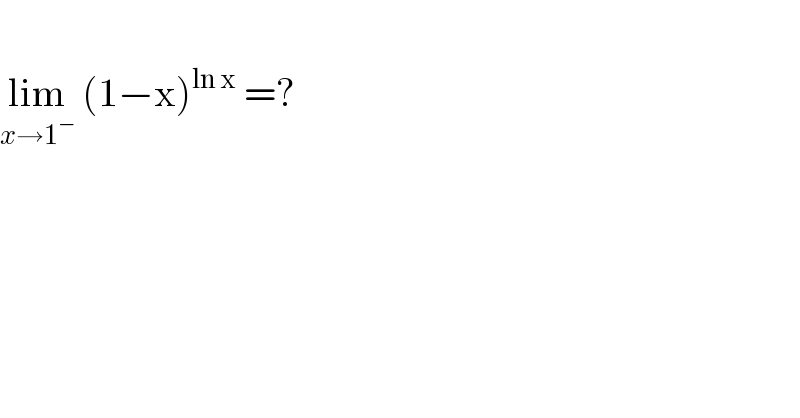
$$ \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{ln}\:\mathrm{x}} \:=?\: \\ $$
Commented by abdomathmax last updated on 06/May/20
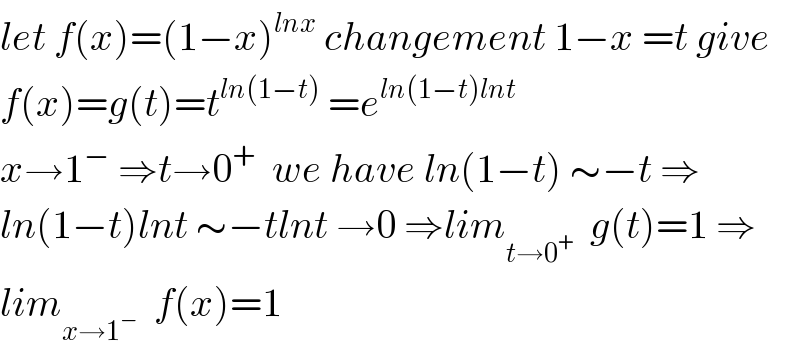
$${let}\:{f}\left({x}\right)=\left(\mathrm{1}−{x}\right)^{{lnx}} \:{changement}\:\mathrm{1}−{x}\:={t}\:{give} \\ $$$${f}\left({x}\right)={g}\left({t}\right)={t}^{{ln}\left(\mathrm{1}−{t}\right)} \:={e}^{{ln}\left(\mathrm{1}−{t}\right){lnt}} \\ $$$${x}\rightarrow\mathrm{1}^{−} \:\Rightarrow{t}\rightarrow\mathrm{0}^{+} \:\:{we}\:{have}\:{ln}\left(\mathrm{1}−{t}\right)\:\sim−{t}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{t}\right){lnt}\:\sim−{tlnt}\:\rightarrow\mathrm{0}\:\Rightarrow{lim}_{{t}\rightarrow\mathrm{0}^{+} } \:\:{g}\left({t}\right)=\mathrm{1}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}^{−} } \:\:{f}\left({x}\right)=\mathrm{1} \\ $$
