Question Number 91813 by jagoll last updated on 03/May/20
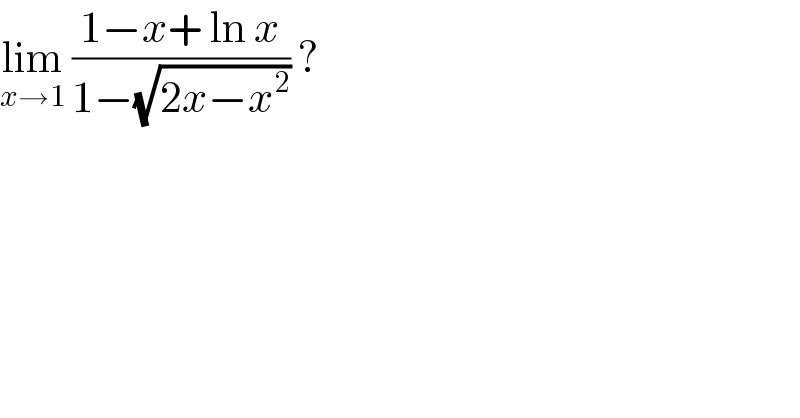
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}−{x}+\:\mathrm{ln}\:{x}}{\mathrm{1}−\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}\:? \\ $$
Commented by john santu last updated on 03/May/20
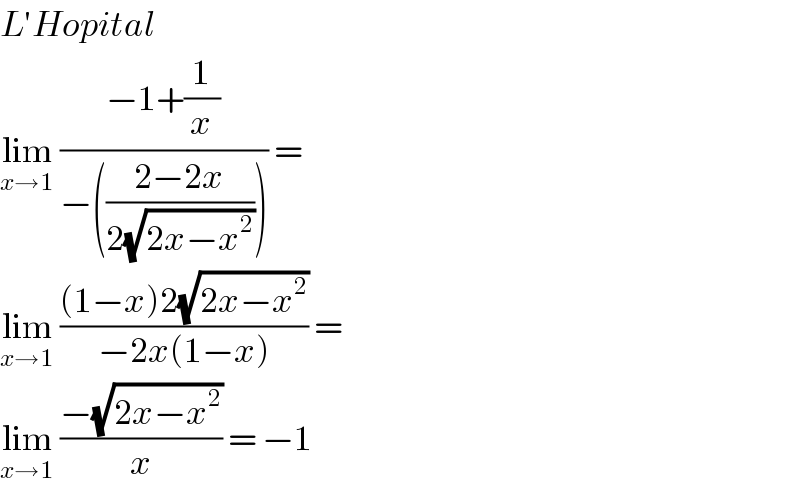
$${L}'{Hopital} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{−\mathrm{1}+\frac{\mathrm{1}}{{x}}}{−\left(\frac{\mathrm{2}−\mathrm{2}{x}}{\mathrm{2}\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}\right)}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}−{x}\right)\mathrm{2}\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}{−\mathrm{2}{x}\left(\mathrm{1}−{x}\right)}\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{−\sqrt{\mathrm{2}{x}−{x}^{\mathrm{2}} }}{{x}}\:=\:−\mathrm{1} \\ $$
Commented by john santu last updated on 03/May/20
������
Commented by jagoll last updated on 03/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
