Question Number 124129 by bramlexs22 last updated on 01/Dec/20
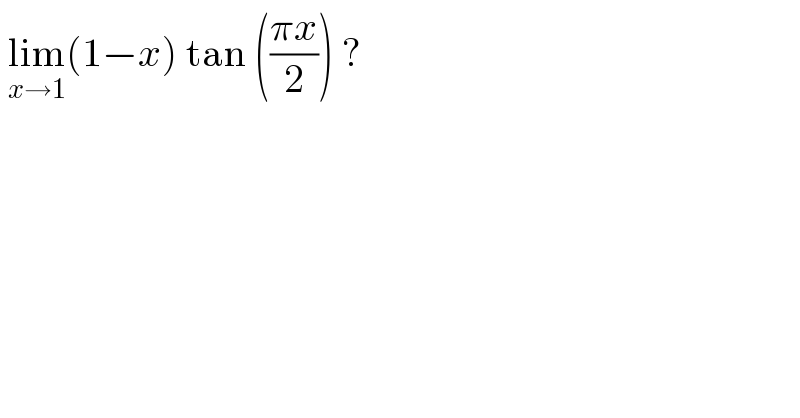
$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\mathrm{1}−{x}\right)\:\mathrm{tan}\:\left(\frac{\pi{x}}{\mathrm{2}}\right)\:? \\ $$
Answered by mathmax by abdo last updated on 01/Dec/20
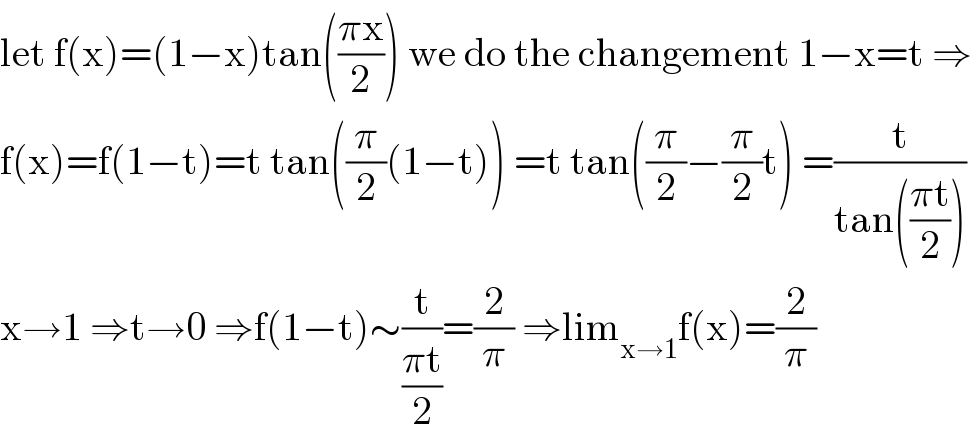
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{1}−\mathrm{x}\right)\mathrm{tan}\left(\frac{\pi\mathrm{x}}{\mathrm{2}}\right)\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{1}−\mathrm{x}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{1}−\mathrm{t}\right)=\mathrm{t}\:\mathrm{tan}\left(\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\mathrm{t}\right)\right)\:=\mathrm{t}\:\mathrm{tan}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}\mathrm{t}\right)\:=\frac{\mathrm{t}}{\mathrm{tan}\left(\frac{\pi\mathrm{t}}{\mathrm{2}}\right)} \\ $$$$\mathrm{x}\rightarrow\mathrm{1}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\:\Rightarrow\mathrm{f}\left(\mathrm{1}−\mathrm{t}\right)\sim\frac{\mathrm{t}}{\frac{\pi\mathrm{t}}{\mathrm{2}}}=\frac{\mathrm{2}}{\pi}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2}}{\pi} \\ $$
Answered by malwan last updated on 01/Dec/20
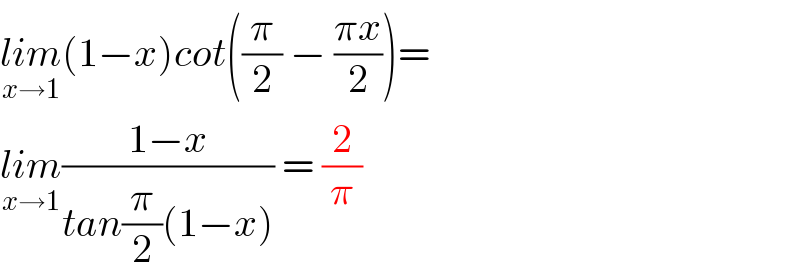
$$\underset{{x}\rightarrow\mathrm{1}} {{lim}}\left(\mathrm{1}−{x}\right){cot}\left(\frac{\pi}{\mathrm{2}}\:−\:\frac{\pi{x}}{\mathrm{2}}\right)= \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {{lim}}\frac{\mathrm{1}−{x}}{{tan}\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{x}\right)}\:=\:\frac{\mathrm{2}}{\pi} \\ $$
