Question Number 129587 by Adel last updated on 16/Jan/21
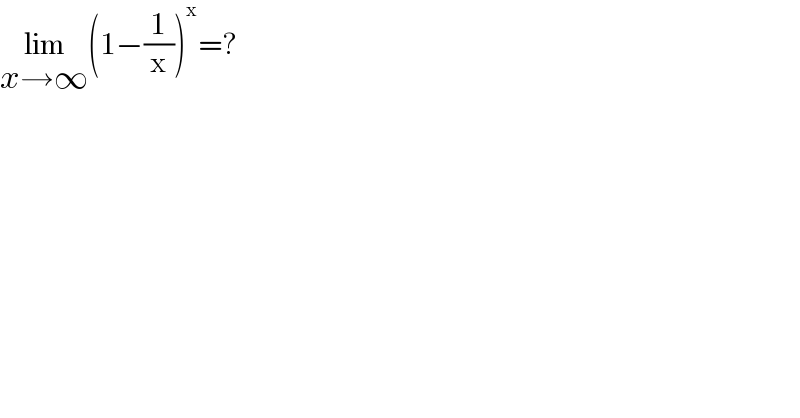
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{x}} =? \\ $$
Answered by Dwaipayan Shikari last updated on 16/Jan/21
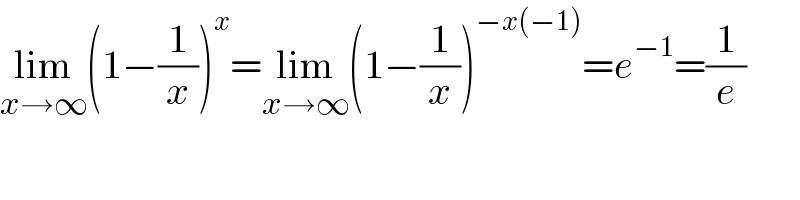
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)^{{x}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)^{−{x}\left(−\mathrm{1}\right)} ={e}^{−\mathrm{1}} =\frac{\mathrm{1}}{{e}} \\ $$
Answered by Ar Brandon last updated on 16/Jan/21
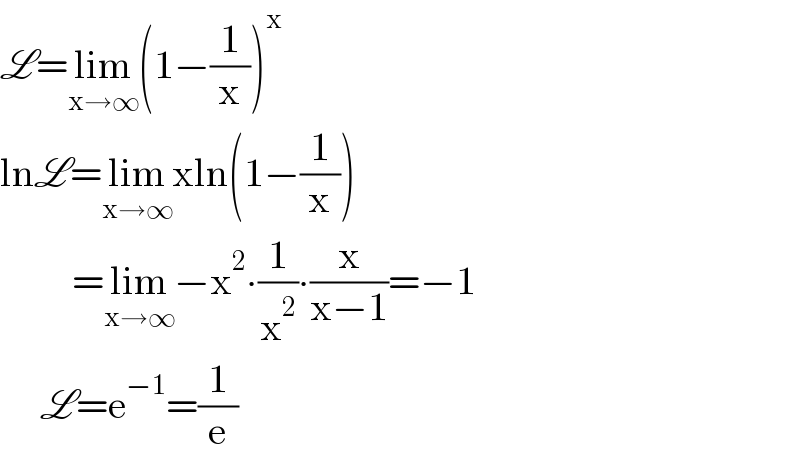
$$\mathscr{L}=\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{x}} \\ $$$$\mathrm{ln}\mathscr{L}=\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}xln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}−\mathrm{x}^{\mathrm{2}} \centerdot\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\centerdot\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}=−\mathrm{1} \\ $$$$\:\:\:\:\:\mathscr{L}=\mathrm{e}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{e}} \\ $$
Answered by physicstutes last updated on 16/Jan/21
![lim_(x→∞) (1−(1/x))^x let −(1/x) = (1/m) m = −x ⇒ x → ∞, m → −∞ lim_(x→−∞) (1+(1/m))^(−m) = lim_(x→−∞) [(1+(1/m))^m ]^(−1) = e^(−1)](https://www.tinkutara.com/question/Q129614.png)
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)^{{x}} \\ $$$$\mathrm{let}\:\:−\frac{\mathrm{1}}{{x}}\:=\:\frac{\mathrm{1}}{{m}} \\ $$$$\:\:\:{m}\:=\:−{x}\:\Rightarrow\:{x}\:\rightarrow\:\infty,\:{m}\:\rightarrow\:−\infty \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{m}}\right)^{−{m}} \:=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{{m}}\right)^{{m}} \right]^{−\mathrm{1}} \:=\:{e}^{−\mathrm{1}} \\ $$
