Question Number 118950 by benjo_mathlover last updated on 21/Oct/20
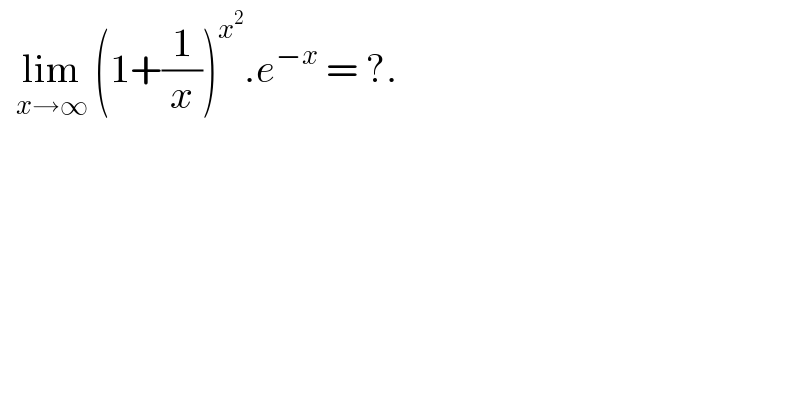
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}^{\mathrm{2}} } .{e}^{−{x}} \:=\:?. \\ $$
Answered by john santu last updated on 21/Oct/20
![L = lim_(x→∞) (((1+(1/x))^x^2 )/e^x ) ln L= lim_(x→∞) ln ((((1+(1/x))^x^2 )/e^x )) ln L = lim_(x→∞) x^2 (ln (1+(1/x))−x) [ by using Maclaurin series ] ln L = lim_(x→∞) x^2 ((1/x)−(1/(2x^2 ))+(1/(3x^3 ))−O(x^3 ))−x) ln L = lim_(x→∞) [x−(1/(2x))+(1/(3x^2 ))−O(x^2 )−x ] ln L = lim_(x→∞) (−(1/2)+(1/(3x^2 ))−O(x^2 ))=−(1/2) L = e^(−(1/2)) = (1/( (√e))) .](https://www.tinkutara.com/question/Q118953.png)
$$\:\mathcal{L}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}^{\mathrm{2}} } }{{e}^{{x}} }\: \\ $$$$\:\mathrm{ln}\:\mathcal{L}=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{ln}\:\left(\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}^{\mathrm{2}} } }{{e}^{{x}} }\right) \\ $$$$\:\mathrm{ln}\:\mathcal{L}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{2}} \left(\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)−{x}\right) \\ $$$$\:\left[\:{by}\:{using}\:{Maclaurin}\:{series}\:\right]\: \\ $$$$\left.\mathrm{ln}\:\mathcal{L}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{3}} }−{O}\left({x}^{\mathrm{3}} \right)\right)−{x}\right) \\ $$$$\:\mathrm{ln}\:\mathcal{L}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\left[{x}−\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }−{O}\left({x}^{\mathrm{2}} \right)−{x}\:\right] \\ $$$$\mathrm{ln}\:\mathcal{L}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }−{O}\left({x}^{\mathrm{2}} \right)\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathcal{L}\:=\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\frac{\mathrm{1}}{\:\sqrt{{e}}}\:. \\ $$$$ \\ $$
