Question Number 122550 by liberty last updated on 18/Nov/20
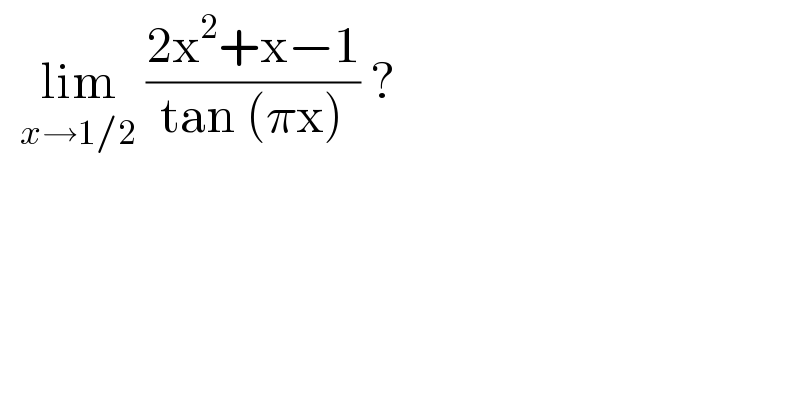
$$\:\:\underset{{x}\rightarrow\mathrm{1}/\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}}{\mathrm{tan}\:\left(\pi\mathrm{x}\right)}\:? \\ $$
Answered by bramlexs22 last updated on 18/Nov/20
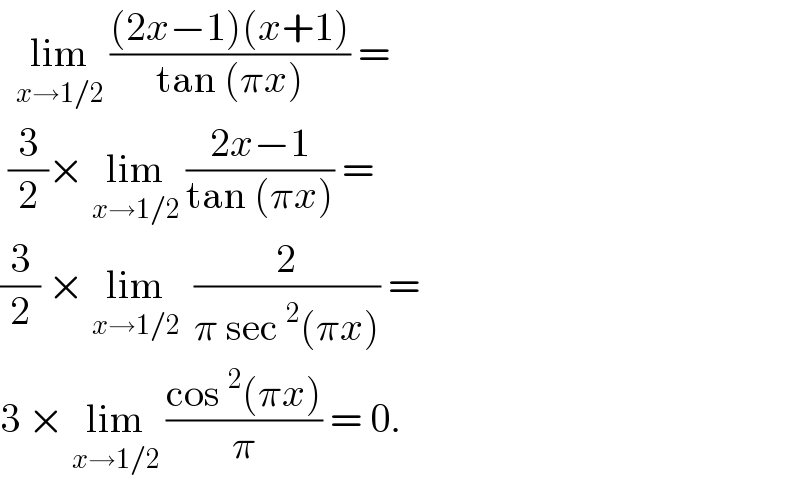
$$\:\:\underset{{x}\rightarrow\mathrm{1}/\mathrm{2}} {\mathrm{lim}}\:\frac{\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}{\mathrm{tan}\:\left(\pi{x}\right)}\:= \\ $$$$\:\frac{\mathrm{3}}{\mathrm{2}}×\:\underset{{x}\rightarrow\mathrm{1}/\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{tan}\:\left(\pi{x}\right)}\:= \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\:×\:\underset{{x}\rightarrow\mathrm{1}/\mathrm{2}} {\mathrm{lim}}\:\:\frac{\mathrm{2}}{\pi\:\mathrm{sec}\:^{\mathrm{2}} \left(\pi{x}\right)}\:= \\ $$$$\mathrm{3}\:×\:\underset{{x}\rightarrow\mathrm{1}/\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:^{\mathrm{2}} \left(\pi{x}\right)}{\pi}\:=\:\mathrm{0}.\: \\ $$
Answered by Dwaipayan Shikari last updated on 18/Nov/20
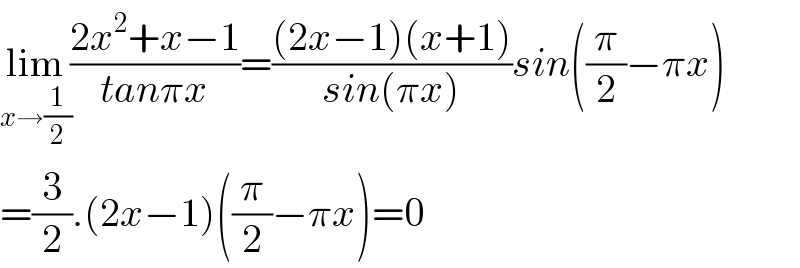
$$\underset{{x}\rightarrow\frac{\mathrm{1}}{\mathrm{2}}} {\mathrm{lim}}\frac{\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{1}}{{tan}\pi{x}}=\frac{\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}{{sin}\left(\pi{x}\right)}{sin}\left(\frac{\pi}{\mathrm{2}}−\pi{x}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}.\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\frac{\pi}{\mathrm{2}}−\pi{x}\right)=\mathrm{0} \\ $$
