Question Number 126195 by bramlexs22 last updated on 18/Dec/20
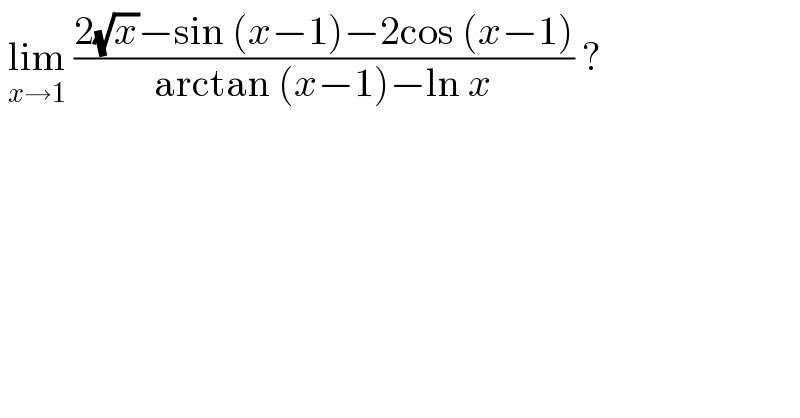
$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{2}\sqrt{{x}}−\mathrm{sin}\:\left({x}−\mathrm{1}\right)−\mathrm{2cos}\:\left({x}−\mathrm{1}\right)}{\mathrm{arctan}\:\left({x}−\mathrm{1}\right)−\mathrm{ln}\:{x}}\:? \\ $$
Answered by liberty last updated on 18/Dec/20

$${let}\:{w}={x}−\mathrm{1}\: \\ $$$${L}=\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\sqrt{{w}+\mathrm{1}}−\mathrm{sin}\:{w}−\mathrm{2cos}\:{w}}{\mathrm{arctan}\:{w}−\mathrm{ln}\:\left({w}+\mathrm{1}\right)} \\ $$$${L}=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left(\mathrm{1}+\frac{{w}}{\mathrm{2}}−\frac{{w}^{\mathrm{2}} }{\mathrm{8}}+{O}\left({w}^{\mathrm{3}} \right)\right)−\left({w}+{O}\left({w}^{\mathrm{3}} \right)\right)−\mathrm{2}\left(\mathrm{1}−\frac{{w}^{\mathrm{2}} }{\mathrm{2}}+{O}\left({w}^{\mathrm{4}} \right)\right)}{\left({w}+{O}\left({w}^{\mathrm{3}} \right)\right)−\left({w}−\frac{{w}^{\mathrm{2}} }{\mathrm{2}}+{O}\left({w}^{\mathrm{3}} \right)\right)} \\ $$$${L}=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{3}{w}^{\mathrm{2}} }{\mathrm{4}}+{O}\left({w}^{\mathrm{3}} \right)}{\:\frac{{w}^{\mathrm{2}} }{\mathrm{2}}+{O}\left({w}^{\mathrm{3}} \right)}\:=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{w}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}+{O}\left({w}\right)\right)}{{w}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}+{O}\left({w}\right)\right)} \\ $$$${L}=\frac{\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{0}}{\:\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{0}}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by bramlexs22 last updated on 18/Dec/20

