Question Number 83710 by john santu last updated on 05/Mar/20
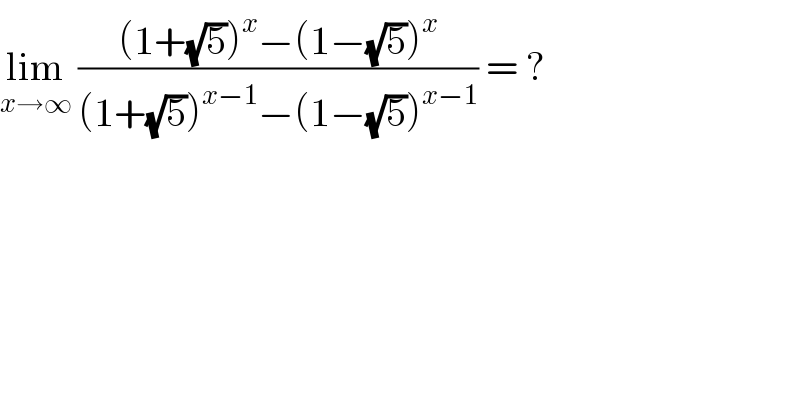
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{{x}} −\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)^{{x}} }{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{{x}−\mathrm{1}} −\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)^{{x}−\mathrm{1}} }\:=\:? \\ $$
Commented by john santu last updated on 05/Mar/20
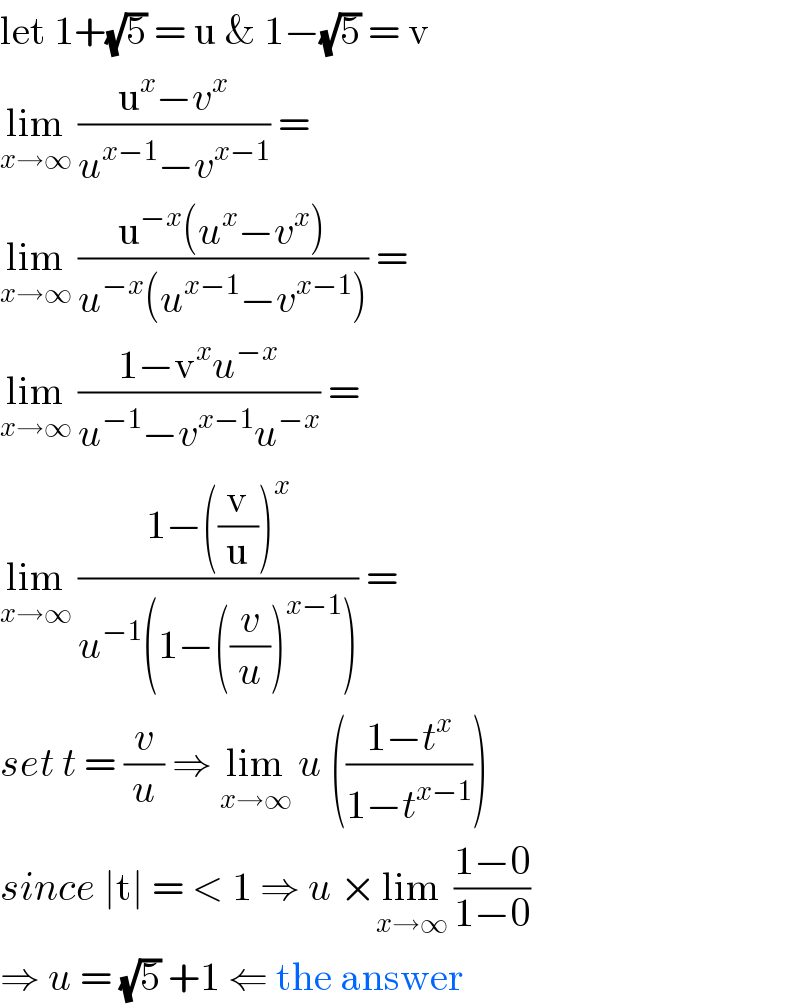
$$\mathrm{let}\:\mathrm{1}+\sqrt{\mathrm{5}}\:=\:\mathrm{u}\:\&\:\mathrm{1}−\sqrt{\mathrm{5}}\:=\:\mathrm{v} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{u}^{{x}} −{v}^{{x}} }{{u}^{{x}−\mathrm{1}} −{v}^{{x}−\mathrm{1}} }\:=\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{u}^{−{x}} \left({u}^{{x}} −{v}^{{x}} \right)}{{u}^{−{x}} \left({u}^{{x}−\mathrm{1}} −{v}^{{x}−\mathrm{1}} \right)}\:=\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{v}^{{x}} {u}^{−{x}} }{{u}^{−\mathrm{1}} −{v}^{{x}−\mathrm{1}} {u}^{−{x}} }\:=\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\frac{\mathrm{v}}{\mathrm{u}}\right)^{{x}} }{{u}^{−\mathrm{1}} \left(\mathrm{1}−\left(\frac{{v}}{{u}}\right)^{{x}−\mathrm{1}} \right)}\:= \\ $$$${set}\:{t}\:=\:\frac{{v}}{{u}}\:\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{u}\:\left(\frac{\mathrm{1}−{t}^{{x}} }{\mathrm{1}−{t}^{{x}−\mathrm{1}} }\right) \\ $$$${since}\:\mid\mathrm{t}\mid\:=\:<\:\mathrm{1}\:\Rightarrow\:{u}\:×\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{0}}{\mathrm{1}−\mathrm{0}}\: \\ $$$$\Rightarrow\:{u}\:=\:\sqrt{\mathrm{5}}\:+\mathrm{1}\:\Leftarrow\:\mathrm{the}\:\mathrm{answer} \\ $$
