Question Number 163961 by qaz last updated on 12/Jan/22

$$\underset{\mathrm{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}} }{\mathrm{x}−\mathrm{1}}=? \\ $$
Answered by bobhans last updated on 12/Jan/22
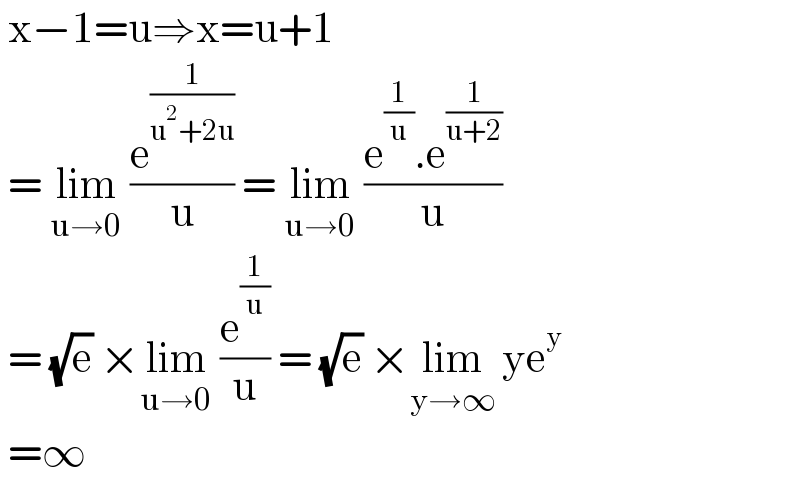
$$\:\mathrm{x}−\mathrm{1}=\mathrm{u}\Rightarrow\mathrm{x}=\mathrm{u}+\mathrm{1} \\ $$$$\:=\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} +\mathrm{2u}}} }{\mathrm{u}}\:=\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{u}}} .\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{u}+\mathrm{2}}} }{\mathrm{u}} \\ $$$$\:=\:\sqrt{\mathrm{e}}\:×\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{u}}} }{\mathrm{u}}\:=\:\sqrt{\mathrm{e}}\:×\underset{\mathrm{y}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{ye}^{\mathrm{y}} \\ $$$$\:=\infty \\ $$
